题目内容
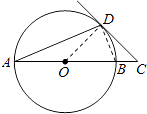
【题目】AB是⊙O的直径,∠DAB=22.5°,延长AB到点C,使得∠ACD=45°. 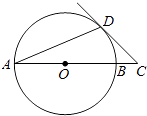
(1)求证:CD是⊙O的切线;
(2)若AB=2 ![]() ,求BC的长.
,求BC的长.
【答案】
(1)证明:连接DO,
∵AO=DO,
∴∠DAO=∠ADO=22.5°.
∴∠DOC=45°.
又∵∠ACD=2∠DAB,
∴∠ACD=∠DOC=45°.
∴∠ODC=90°.
又 OD是⊙O的半径,
∴CD是⊙O的切线
(2)解:连接DB,
∵直径AB=2 ![]() ,△OCD为等腰直角三角形,
,△OCD为等腰直角三角形,
∴CD=OD= ![]() ,OC=
,OC= ![]() =2,
=2,
∴BC=OC﹣OB=2﹣ ![]() .
.
【解析】(1)连接DO,由三角形的外角与内角的关系易得∠DOC=∠C=45°,故有∠ODC=90°,即CD是圆的切线.(2)由1知,CD=OD= ![]() AB,由弦切角定理可得∠CDB=∠A,故有△ADC∽△DBC,得到CD2=CBCA=CB(CB+AB)而求得BC的值.
AB,由弦切角定理可得∠CDB=∠A,故有△ADC∽△DBC,得到CD2=CBCA=CB(CB+AB)而求得BC的值.
【考点精析】利用圆周角定理和切线的判定定理对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

练习册系列答案
相关题目