题目内容
如图,直线AB分别x,y轴正半轴相交于A(a,0)和B(0,b),直 线y=
线y=
x+3交于y轴与点E,交AB于点F
(1)当a=6,b=6时,求四边形EOAF的面积
(2)若F为线段AB的中点,且AB=4
时,求证:∠BEF=∠BAO.
 线y=
线y=| 1 |
| 2 |
(1)当a=6,b=6时,求四边形EOAF的面积
(2)若F为线段AB的中点,且AB=4
| 5 |
(1)y=
x+3,
当x=0时,y=3,
∴E(0,3),
设直线AB的解析式是y=kx+b,
把A(6,0),B(0,6)代入y=kx+b得:
,
解得:
∴直线AB的函数关系式是y=-x+6
直线EFy=
x+3和直线AB交于点F,方程组
的解是
,
∴F(2,4),
S四边形EOAF=S△OAB-S△EFB,
=
×6×6-
×(6-3)×2,
=15.
所以四边形EOAF的面积是15.
(2)∵F为线段AB的中点,由三角形中位线定理得F(
a,
b),
又∵F在直线EF:y=
x+3上,
∴
×
a+3=
b,
a=2b-12 ①
又∵AB=4
∴a2+b2=(4
)2,
∴(2b-12)2+b2=80,
整理得:5b2-48b+64=0,
解得b1=
,b2=8,
当b=
时,a<0,不合题意,∴b=
(舍去),
当b=8时,a=4
∴A(4,0)B(0,8),
∴OE=3,BE=5
连接EA,在RT△OAE中,OE=3,OA=4,
∴EA=5
∴EA=BE=5
∴△BEA是等腰三角形,
又∵F为线段AB的中点
∴EF⊥AB,
∴∠BEF=90°-∠EBF,
∠BAO=90°-∠OBA,
∵∠EBF=∠OBA
∴∠BEF=∠BAO.
| 1 |
| 2 |
当x=0时,y=3,
∴E(0,3),
设直线AB的解析式是y=kx+b,
把A(6,0),B(0,6)代入y=kx+b得:
|
解得:
|
∴直线AB的函数关系式是y=-x+6
直线EFy=
| 1 |
| 2 |
|
|
∴F(2,4),
S四边形EOAF=S△OAB-S△EFB,
=
| 1 |
| 2 |
| 1 |
| 2 |
=15.
所以四边形EOAF的面积是15.
(2)∵F为线段AB的中点,由三角形中位线定理得F(
| 1 |
| 2 |
| 1 |
| 2 |
又∵F在直线EF:y=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
a=2b-12 ①
又∵AB=4
| 5 |
∴a2+b2=(4
| 5 |
∴(2b-12)2+b2=80,
整理得:5b2-48b+64=0,
解得b1=
| 8 |
| 5 |
当b=
| 8 |
| 5 |
| 8 |
| 5 |
当b=8时,a=4
∴A(4,0)B(0,8),
∴OE=3,BE=5
连接EA,在RT△OAE中,OE=3,OA=4,
∴EA=5
∴EA=BE=5
∴△BEA是等腰三角形,
又∵F为线段AB的中点
∴EF⊥AB,
∴∠BEF=90°-∠EBF,
∠BAO=90°-∠OBA,
∵∠EBF=∠OBA
∴∠BEF=∠BAO.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
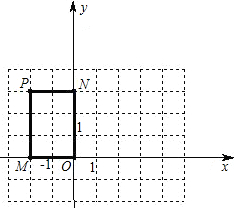 形PMON沿x轴正方向平移4个单位,得到矩形P′M′O′N′(P?P′,M?M′,O?O′,N?N′)
形PMON沿x轴正方向平移4个单位,得到矩形P′M′O′N′(P?P′,M?M′,O?O′,N?N′)




