Question

已知平面直角坐标系内，一次函数y=kx+2的图象与x轴相交于点A(-2

3

，0)，与y轴相交于点B．
（1）求一次函数的解析式，并在直角坐标系中画出它的图象；
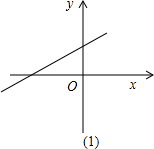
（2）若以原点O为圆心的⊙O与直线AB相切于点C，求⊙O的半径和点C的坐标；
（3）在x轴上是否存在点P，使△PAB为等腰三角形？若存在，请写出点P的坐标；若不存在，请说明理由．

Answer 1

（1）∵一次函数y=kx+2的图象与x轴相交于A，
∴把点A(-2

3

，0)代入y=kx+2得：
-2

3

k+2=0，
k=

3

3

，
∴一次函数的解析式：y=

3

3

x+2；

（2）过点O作OC⊥AB于C，
∵一次函数的解析式：y=

3

3

x+2，
∴它与y轴的交点坐标为（0，2），
∴OA=2

3

，OB=2，
∴tan∠OAB=

3

3

∴∠OAB=30°
∴在Rt△CAB中，OC=

1

2

OA=

3

，
∴⊙O的半径为

3

，
过点C作CD⊥OA于D，
∴CD=

3

2

，OD=

3

2

，
∴点C的坐标为（-

3

2

，

3

2

）

（3）在x轴上存在点P，使△PAB为等腰三角形，
由题意得，AB=4
当以A为顶角的顶点时，P（-4-2

3

，0），
当以B为顶角的顶点时，P（2

3

，0），
当以AB为腰时，P（-

2 3

3

，0）