题目内容
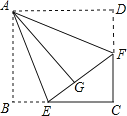
【题目】如图，在梯形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点在BC上，且四边形AEFD是平行四边形．
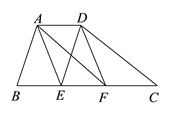
（1）AD与BC有何等量关系？请说明理由；
（2）当AB=DC时，求证：四边形AEFD是矩形．
【答案】（1）AD=
BC；（2）见解析.
【解析】分析：
（1）由AD∥BC，AB∥DE，AF∥DC，易得四边形ABED和四边形AFCD都是平行四边形，结合四边形AEFD是平行四边形可得AD=BE=EF=FC，由此可得AD=BC；
（2）由（1）可知四边形ABED和四边形AFCD都是平行四边形，从而可得AB=DE，AF=DC结合AB=CD可得DE=AF，再结合四边形AEFD是平行四边形即可得到四边形AEFD是矩形的结论.
详解：
（1）∵AD∥BC，AB∥DE，AF∥DC，
∴四边形ABED和四边形AFCD都是平行四边形，
∴AD=BE，AD=CF，
∵四边形AEFD是平行四边形，
∴AD=EF，
∴AD=BE=EF=FC，
∴BC=BE+EF+FC=3AD，
∴AD=BC；
（2）∵四边形ABED和四边形AFCD都是平行四边形，
∴DE=AB，AF=CD，
又∵AB=CD，
∴AF=DE，
又∵四边形AEFD是平行四边形，
∴平行四边形AEFD是矩形.
练习册系列答案
相关题目
