题目内容
【题目】已知:在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,且∠ACB=90°,AC=BC.
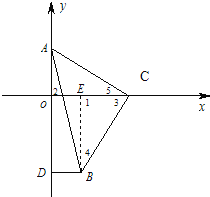
(1)如图1,当A(0,-2),C(1,0),点B在第四象限时,求点B的坐标;
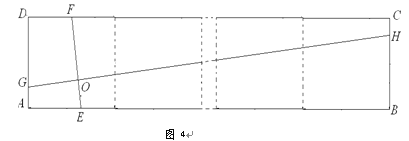
(2)如图2,当点C在x轴正半轴上运动,点A在y轴正半轴上运动,点B在第四象限时,作BD⊥y轴于点D,试判断![]() 是一个定值,并说明定值是多少?请证明你的结论.
是一个定值,并说明定值是多少?请证明你的结论.
【答案】(1)(3,-1);(2)![]()
【解析】
(1)过B作BE⊥x轴于E,推出∠2=∠OAC,∠AOC=∠BEC,根据AAS证△AOC≌△CEB,推出OA=CE,OC=BE,根据A、C的坐标即可求出答案;
(2)作BE⊥x轴于E,得出矩形OEBD,推出BD=OE,证△CEB≌△AOC,推出AO=CE,求出OC-BD=OA,代入求出即可.
解:(1) 过B作BE⊥x轴于E,
则∠BEC=∠ACB=∠AOC=90°,
∴∠1+∠2=90°,∠1+∠OAC=90°,
∴∠2=∠OAC,
在△AOC和△CEB中
∵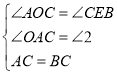 ,
,
∴△AOC≌△CEB(AAS),
∴OA=CE,OC=BE,
∵A(0,-2),C(1,0),
∴OA=CE=2,OC=BE=1,
∴OE=1+2=3,
∴点B的坐标为(3,-1);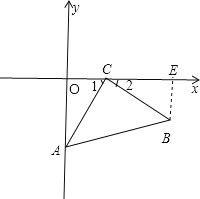
(2)结论:![]()
证明:作BE⊥x轴于E,
∴∠1=90°=∠2,
∴∠3+∠4=90°,
∵∠ACB=90°,
∴∠5+∠3=90°,
∴∠5=∠4,
在△CEB和△AOC中,
∵
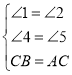
∴△CEB≌△AOC,
∴AO=CE,
∵BE⊥x轴于E,
∴BE∥y轴,
∵BD⊥y轴于点D,EO⊥y轴于点O,
∴BD∥OE,
∴四边形OEBD是长方形,
∴EO=BD,
∴OC-BD=OC-EO=CE=AO,
∴![]()

练习册系列答案
相关题目