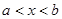题目内容
关于二次函数y=x2-4x+3,下列说法错误的是( )
| A.当x<1时,y随x的增大而减小 | B.它的图象与x轴有交点 |
| C.当1<x<3时,y>0 | D.顶点坐标为(2,-1 ) |
C.
解析试题分析:根据二次函数的性质解题.
在函数y=x2-4x+3中a=1>0,
∴此函数图象开口向上;
又∵a=1,b=-4,c=3,
∴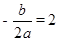 ,
,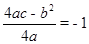 .
.
∴顶点坐标是(2,-1),且对称轴是x=2,
∴故D正确;
∴令x2-4x+3=0,
解得x1=1,x2=3,
∴此函数图象和x轴有交点,求交点坐标是(1,0);(3,0).
故B正确;
当x<1时,即说明x的取值范围在对称轴的左边,
∴y随x的增大而减小,故A正确;
当1<x<3时,y的值在x轴下方,∴y<0,故C错误.
故选C.
考点: 二次函数的性质.

练习册系列答案
相关题目
已知二次函数y=ax²+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )
| A.a>0 | B.3是方程ax²+bx+c=0的一个根 |
| C.a+b+c=0 | D.当x<1时,y随x的增大而减小 |
抛物线y=x2向上平移2个单位,得到新抛物线的函数表达式是( )
| A.y=x2-2 | B.y=(x-2)2 | C.y=x2+2 | D.y=(x+2)2 |
如果将抛物线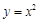 向左平移2个单位,那么所得抛物线的表达式为( )
向左平移2个单位,那么所得抛物线的表达式为( )
A. | B.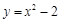 | C.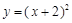 | D.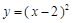 |
抛物线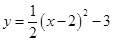 的顶点坐标是( )
的顶点坐标是( )
A.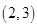 | B.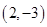 | C.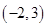 | D.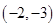 |
如右图,已知二次函数y=ax2+bx+c的图象过A(-3,0),对称轴为直线x=-1,下列结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b;⑤a-b>m(am+b)(m≠-1)其中正确的结论有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
二次函数 的图象的顶点坐标是( )
的图象的顶点坐标是( )
| A.(-1,3) | B.(-1,-3) | C.(1,-3) | D.(1,3) |
 (a为常数,且a≠0),图像的顶点为C.以下三个判断: ①无论a为何值,该函数的图像与x轴一定有两个交点;②无论a为何值,该函数的图像在x轴上截得的线段长为1;③若该函数的图像与x轴有两个交点A、B,且S△ABC=1时,则a=8.其中,正确的是( )
(a为常数,且a≠0),图像的顶点为C.以下三个判断: ①无论a为何值,该函数的图像与x轴一定有两个交点;②无论a为何值,该函数的图像在x轴上截得的线段长为1;③若该函数的图像与x轴有两个交点A、B,且S△ABC=1时,则a=8.其中,正确的是( ) 的一元二次方程
的一元二次方程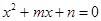 的两个实数根分别为
的两个实数根分别为 ,
,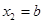 (
( ),则二次函数
),则二次函数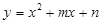 中,当
中,当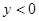 时,
时,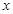 的取值范围是( )
的取值范围是( )