题目内容
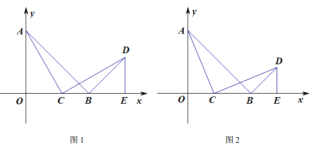
【题目】如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点BC重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)当D在线段BC上时,求证:△BAD≌△CAE;
(2)当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数(直接写出结果,无需写出求解过程).

【答案】(1)见解析(2) 当点D运动到BC中点时,AC⊥DE. (3) ∠ADB的度数是![]() 或
或![]() 或
或![]()
【解析】
(1)根据∠DAE=∠BAC,得到![]() 根据SAS即可判定△BAD≌△CAE;
根据SAS即可判定△BAD≌△CAE;
(2) 当点D运动到BC中点时,AC⊥DE.
(3) △ABD中最小角为20°,分三种情况进行讨论即可.
(1)![]() ∠DAE=∠BAC,
∠DAE=∠BAC,
![]()
即![]()
在△BAD和△CAE中,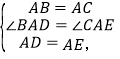
△BAD≌△CAE![]() ,
,
(2) 当点D运动到BC中点时,AC⊥DE.
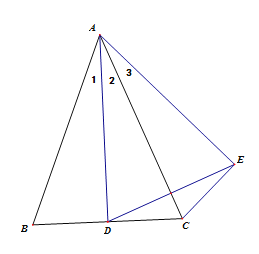
![]() D运动到BC中点,
D运动到BC中点,
AB=AC,
![]()
![]() △BAD≌△CAE
△BAD≌△CAE
![]()
![]()
![]()
![]() AC⊥DE.
AC⊥DE.
![]() 当点D运动到BC中点时,AC⊥DE.
当点D运动到BC中点时,AC⊥DE.
(3) ∠ADB的度数是![]() 或
或![]() 或
或![]()

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目