Question

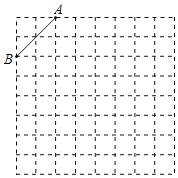
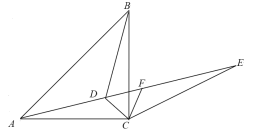
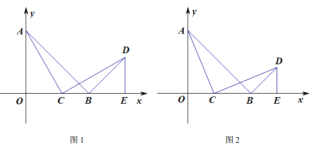
【题目】如图1，在平面直角坐标系中，，点的坐标为，，点为线段上的动点（点不与、重合），连接，作，且，过点作轴，垂足为点.

（1）求证：；

（2）猜想的形状并证明结论；

（3）如图2，当为等腰三角形时，求点的坐标.

Answer 1

【答案】（1）见解析；（2）为等腰直角三角形，理由见解析；（3）点的坐标为

【解析】

（1）根据垂直的定义得到∠ACD＝90°，根据余角的性质得到∠ACO＝∠CDE，根据全等三角形的判定定理即可得到结论；

（2）根据全等三角形的性质得到AO＝CE，CO＝DE，求得OB＝CE，得到OC+CB＝BE+CB，由等腰直角三角形的判定定理即可得到结论；

（3）设D点的纵坐标为m，当△BCD为等腰三角形时，①BC＝BD，②CD＝BD＝m，③当CD＝BC＞CE，根据题意列方程即可得到结论．

解：（1）∵，

∴，

∴，

∵轴，，

∴，

∴，

∴.

在和中，

，

∴.

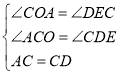（2）为等腰直角三角形.

理由如下：

∵，

∴，，

∵，

∴，

∴，

即，

∵，

∴为等腰直角三角形.

（3）设D点的纵坐标为m，
当△BCD为等腰三角形时，
①BC=BD，∵△BDE是等腰直角三角形，
∴DE=BE=m，
∴BD=BC=m，
∵CE=AO=1，
∴m+m=1，
∴m=-1，
∴D（，-1）；
②CD=BD=m，
∵OC=DE=m，
∴AC=CD==m，
解得：m=±1（舍去），
③当CD=BC＞CE（这种情况不存在），
综上所述，当△BCD为等腰三角形时，点D的坐标（，-1）．