题目内容
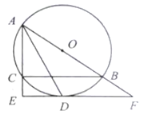
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() 与y轴交于点C,抛物线
与y轴交于点C,抛物线![]() 经过点B,C,与x轴的另一个交点为A.
经过点B,C,与x轴的另一个交点为A.
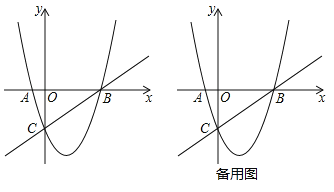
(1)求抛物线的解析式;
(2)点P是直线![]() 下方抛物线上一动点,求四边形
下方抛物线上一动点,求四边形![]() 面积最大时点P的坐标;
面积最大时点P的坐标;
(3)若M是抛物线上一点,且![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.
【答案】(1)y=![]() ;(2)P(2,-3);(3)点P为(3,-2)或(
;(2)P(2,-3);(3)点P为(3,-2)或(![]() ,
,![]() )
)
【解析】
(1)将点B坐标代入直线,求出c的值,并求得点C的坐标,将点B、C代入抛物线可求得解析式;
(2)因为S四边形ACPB=S△ABC+S△PCB,又因为S△ABC是常数,故四边形面积最大,只需要S△PCB最大即可;
(3)存在2种情况,一种是点M在CB下方,根据平行可得点M的坐标;另一种是点M在CB上方,如图,利用NB=NC来求解.
(1)∵直线过点B(4,0)
∴0=![]() ,解得:c=-2
,解得:c=-2
∴直线的解析式为:y=![]()
∵点C是直线与y轴的交点
∴C(0,-2)
将B(4,0)、C(0,-2)代入抛物线得:
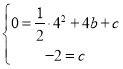
解得:c=-2,b=![]()
∴抛物线的解析式为:y=![]() ;
;
(2)如下图,过点P作x轴的垂线,交CB于点H,交x轴于点G,连接CP、PB

∵S四边形ACPB=S△ABC+S△PCB,
又∵S△ABC是常数,
∴要想四边形面积最大,只需要S△PCB最大
设点P(x,![]() )
)
由图形可知,S△CPB=S△CPH+S△PHB
在△CPH中,以HP为底,则点C到HP的距离为高,即OG的长
在△PHB中,以HP为底,则点B到HP的距离为高,即GB的长
∴![]()
∵A(-1,0),B(4,0),∴OB=4
∵点P(x,![]() )
)
∴点H(x,![]() )
)
∴HP=![]() +2x
+2x
∴![]() =
=![]()
∵-1<0,∴![]() 有最大值,此时,x=
有最大值,此时,x=![]()
则点P(2,-3);
(3)情况一:如下图,点M在CB下方
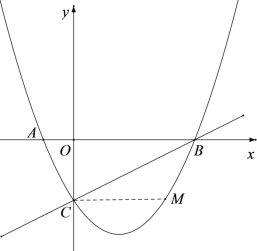
∵∠ABC=∠BCM
∴AB∥CM
∴点M的纵坐标与点C的纵坐标相等
∴点M的纵坐标为-2,代入抛物线得:
-2=![]()
解得:x=0(舍)或x=3
∴点P(3,-2);
情况二:如下图,点M早CB上方,连接CM交x轴于点N
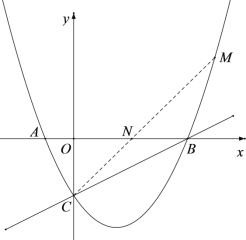
∵∠MCB=∠ABC
∴△NCB是等腰三角形,NB=NC,∴![]()
设点M(m,![]() )
)
∵点C(0,-2)
∴MC所对应的直线解析式为:y=![]()
令y=0,解得x=![]()
∴N(![]() ,0)
,0)
∴NB=4-![]() ,
,![]()
∵点C(0,-2),点N(![]() ,0)
,0)
∴![]() +
+![]()
∴![]() +
+![]()
解得:m=![]()
∴P(![]() ,
,![]() )
)
综上得:点P为(3,-2)或(![]() ,
,![]() ).
).

【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元. (两种方式每次进园均指单人)
元. (两种方式每次进园均指单人)
设进园次数为![]() (
(![]() 为非负整数)
为非负整数)
![]() 根据题意,填写下表:
根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) | 200 |
![]() 设方式一收费
设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 当
当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.