题目内容
【题目】如图,在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为_______cm.

【答案】4.8;
【解析】
连接AP,先利用勾股定理的逆定理证明△ABC为直角三角形,∠BAC=90°,再证明四边形AEPF为矩形,则AP=EF,当AP的值最小时,EF的值最小,利用垂线段最短得到AP⊥BC时,AP的值最小,然后利用面积法计算此时AP的长即可.
解:
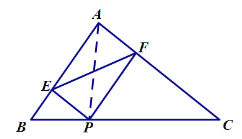
连接AP,
∵AB=6cm,AC=8cm,BC=10cm,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,
∴∠BAC=90°,
又∵PE⊥AB,PF⊥AC,
∴四边形AEPF是矩形,
∴AP=EF,
当AP⊥BC时,EF的值最小,
SABC=![]() AB×AC=
AB×AC=![]() BC×AP
BC×AP
则:![]() ×6×8=
×6×8=![]() ×10×AP,
×10×AP,
解得AP=4.8cm.
∴EF的最小值是4.8cm.
答案为4.8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目