��Ŀ����
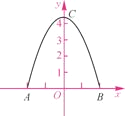
����Ŀ����ͼ����֪������y=ax2+bx+c��x���һ������A������Ϊ����1��0�����Գ���Ϊֱ��x=��2��
��1������������x�����һ������B�����ꣻ
��2����D����������y��Ľ��㣬��C���������ϵ���һ�㣮��֪��ABΪһ�ױߵ�����ABCD�����Ϊ9����������ߵĽ���ʽ����ָ������E�����ꣻ
��3����P�ǣ�2���������߶Գ�����һ���㣬����1����λ/����ٶȴӴ������ߵĶ���E�����˶������P�˶���ʱ��Ϊt�룮
����tΪ�� ����ʱ����PAD���ܳ���С����tΪ�� ����ʱ����PAD����ADΪ���ĵ��������Σ�������������ţ�
����P���˶������У��Ƿ����һ��P��ʹ��PAD����ADΪб�ߵ�ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡��⣺��1���������ߵ���Գ��Լ�A����1��0�����ɵ�B����3��0����
��2���������ߵĶԳ��ύCD�ڵ�M����AB�ڵ�N��
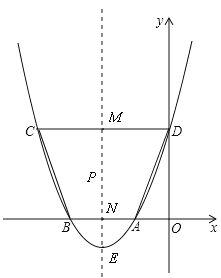
�������֪AB��CD���������ߵ���Գ��Կɵ�CD=2DM��
��MN��y�ᣬAB��CD�����ı���ODMN�Ǿ��Ρ�
��DM=ON=2����CD=2��2=4��
��A����1��0����B����3��0������AB=2��
������ABCD�����=![]() ��AB+CD��OD=9��
��AB+CD��OD=9��
��OD=3����c=3��
��A����1��0����B����3��0������y=ax2+bx+3��
![]() �����
�����![]() ��
��
��y=x2+4x+3��
��y=x2+4x+3��Ϊ����ʽΪy=��x+2��2��1����E����2����1������
��3����2�� 4��![]() ��
��![]() ��
��
�����ڡ�
�ߡ�APD=90�㣬��PMD=��PNA=90�㣬���PDM+��APN=90�㣬��DPM+��PDM=90�㡣
���PDM=��APN��
�ߡ�PMD=��ANP�����APN�ס�PDM��
��![]() ����
����![]() ��
��
��PN2��3PN+2=0�����PN=1��PN=2��
��P����2��1����2��2����
��������
������1�����������ߵ���Գ��Կɵ���������x�����һ������B��������
��2���ȸ�������ABCD�����Ϊ9������c��ֵ�������ô���ϵ�������������ߵĽ���ʽ��ת��Ϊ����ʽ����E��������
��3����������ԳƩ����·��������ɵ���PAD���ܳ���Сʱt��ֵ�����ݵ��������ε����ʿɷ�������������PAD����ADΪ���ĵ���������ʱt��ֵ��
����֤����APN�ס�PDM���������������ε��������PN��ֵ���Ӷ��õ���P��������

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�