题目内容
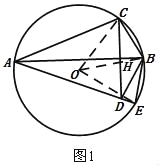
【题目】如图，四边形ACBE内接于⊙O，AB平分∠CAE，CD⊥AB交AB、AE分别于点H、D．
（1）如图①，求证：BD=BE；
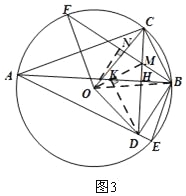
（2）如图②，若F是弧AC的中点，连接BF，交CD于点M，∠CMF=2∠CBF，连接FO、OC，求∠FOC的度数；
（3）在（2）的条件下，连接OD，若BC=4
，OD=7，求BF的长．
【答案】（1）详见解析；（2）∠FOC=60°；（3）BF=13．
【解析】
试题分析：（1）如图1，连接半径OB、OC、OE，由角平分线得：∠CAB=∠BAE，在同圆或等圆中，圆周角相等，则所对的圆心角也相等，得∠COB=∠BOE，所以所对的弦相等：BC=BE，证明△ACH≌△ADH，AB为线段CD的垂直平分线，得BC=BD，则BD=BE；（2）由弧相等，所对的圆周角相等得：∠CBF=∠ABF，由已知中的∠CMF=2∠CBF，得∠BMH=2∠ABF，求得∠CBF=30°，所以∠FOC=2∠CBF=60°；（3）如图3，连接OM，OB，作ON⊥BF于N，DK⊥OM于K，由（2）中的30°和BC=4
分别求出：BH=2，CH=6，BM=4 HM=2，再证明△OMC≌△OMB，得∠CMO=∠BMO=120°，∠OMF=∠OMD=60°，由DM=8可以求MK和DK的长，由勾股定理列式求OK=1，OM=5，求出BN的长，利用垂径定理可得结论：BF=2BN=13．
试题解析：（1）如图1，连接OB、OC、OE，
∵AB平分∠CAE，
∴∠CAB=∠BAE，
∴∠COB=∠BOE，
∴BC=BE，
∵CD⊥AB，
∴∠CHA=∠DHA=90°，
∵∠CAB=∠BAE，AH=AH，
∴△ACH≌△ADH，
∴CH=DH，
∴AB为线段CD的垂直平分线，
∴BC=BD，
∴BD=BE；
（2）∵F是弧AC的中点，
∴
，
∴∠CBF=∠ABF，
∵∠CMF=2∠CBF，
∴∠CMF=2∠ABF，
∵CD⊥AB，∠CMF=∠BMH，
∴∠BMH+∠ABF=90°，
∴∠ABF=30°，
∴∠CBF=30°，
∵∠FOC=2∠CBF，
∴∠FOC=60°；
（3）如图3，连接OM，OB，作ON⊥BF于N，DK⊥OM于K，
由（2）可知：∠CBF=∠ABF=∠BCH=30°，
∴CM=BM，
在Rt△CBH中，∠BCH=30°，BC=4，
∴BH=2，CH=6，
在Rt△BHM中，∠MBH=30°，BH=2，
∴BM=4 HM=2，
∴CM=BM=4，
∵OC=OB，OM=OM，
∴△OMC≌△OMB，
∴∠CMO=∠BMO=120°，∠OMF=∠OMD=60°，
∵CH=DH=6，
∴DM=8，
在Rt△DMK中，∠KMD=60°，DM=8，
∴MK=4，DK=4，
在Rt△OKD中，
OD2=OK2+DK2，
∵OD=7，DK=4，
∴OK=1，
∴OM=5，
在Rt△OMN中，∠OMN=60°，OM=5，
MN=
OM=
，
∴BN=BM+MN=
，
∵ON⊥BF，
∴BF=2BN=13．
