题目内容
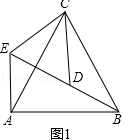
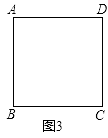
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是线段CB上的异于B、C的动点,AF⊥AE交线段CD的延长线于点F,EF与AD交于点M.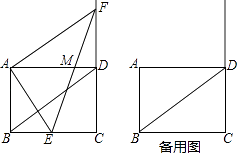
(1)求证:△ABE∽△ADF;
(2)若AE⊥BD,求BE长;
(3)若△AEM是以AE为腰的等腰三角形,求BE的长.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠C=∠ADC=∠ADF=90°,AD∥BC,
∵AF⊥AE,∴∠EAF=90°,
∴∠BAD=∠EAF,
∴∠BAE=∠DAF,
∵∠ABE=∠ADF=90°,
∴△ABE∽△ADF
(2)
解:∵AD∥BC,
∴∠AEB=∠DAE,
∵AE⊥BD,
∴∠BAE+∠ABD=90°,
∵∠BAE+∠AEB=90°,
∴∠ABD=∠AEB,
∴∠AEB=∠ABD,
又∵∠ABE=∠BAD=90°,
∴△ABE∽△DAB,
∴ ![]() ,即
,即 ![]() ,
,
解得:BE= ![]()
(3)
解:分两种情况:
①当AE=AM时,∠AEF=∠AME,
∵AF⊥AE,
∴∠EAF=90°,
∵AD∥BC,
∴∠AME=∠CEF,
∴∠AEF=∠CEF,
在△AEF和△CEF中,  ,
,
∴△AEF≌△CEF(AAS),
∴AE=CE,
设BE=x,则AE=CE=4﹣x,Rt△ABE中,
由勾股定理得:x2+32=(4﹣x)2,解得:x= ![]() ;
;
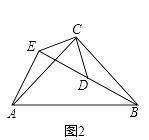
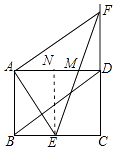
②当AE=EM时,过点E作EN⊥AD于点N,如图所示:
则AN=MN=BE=x,EN∥DF,
由(1)得:△ABE∽△ADF,
∴ ![]() ,即
,即 ![]() ,
,
解得:DF= ![]() x,
x,
∵EN∥DF,
∴∴△EMN∽△FMD,
∴ ![]() ,即
,即 ![]() ,
,
解得:x= ![]() 或x=﹣6(舍去),
或x=﹣6(舍去),
∴BE= ![]() ;
;
综上所述,若△AEM是以AE为腰的等腰三角形,BE长为 ![]() 或
或 ![]() .
.
【解析】(1)由矩形的性质得出∠BAD=∠ABC=∠C=∠ADC=∠ADF=90°,AD∥BC,证出∠BAE=∠DAF,即可得出结论;(2)证明△ABE∽△DAB,得出对应边成比例,即可得出答案;(3)①当AE=AM时,证明△AEF≌△CEF(AAS),得出AE=CE,设BE=x,则AE=CE=4﹣x,Rt△ABE中,由勾股定理得出方程,解方程即可;②当AE=EM时,过点E作EN⊥AD于点N,则AN=MN=BE=x,EN∥DF,由(1)得:△ABE∽△ADF,得出对应边成比例求出DF= ![]() x,由平行线证明△EMN∽△FMD,得出对应边成比例,得出方程,解方程即可.
x,由平行线证明△EMN∽△FMD,得出对应边成比例,得出方程,解方程即可.
【考点精析】认真审题,首先需要了解相似三角形的应用(测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解).

【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?