Question

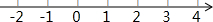（2012•太原二模）（1）解不等式

2x-1

3

-

5x+1

2

≤1，并把它的解集表示在数轴上．
（2）已知抛物线y=ax²+2x+c经过点A（2，5）和点B（-1，-4），求该抛物线的表达式．并说出它是由抛物线y=ax²经过怎样的平移得到的．

Answer 1

分析：（1）不等式左右两边同时乘以6去分母后，去括号合并整理后，将x的系数化为1，求出不等式的解集，将解集表示在数轴即可；
（2）将A与B的坐标代入抛物线解析式中，得到关于a与c的方程组，求出方程组的解得到a与c的值，确定出抛物线解析式，将解析式化为顶点形式，即可得到它是由抛物线y=x²向左平移1个单位，向下平移4个单位得到的．

解答：解：（1）原不等式去分母得：4x-2-（15x+3）≤6，
去括号得：4x-2-15x-3≤6，
整理得：-11x≤11，
解得：x≥-1，
在数轴上表示如下：


（2）∵抛物线y=ax²+2x+c经过点A（2，5）和点B（-1，-4），
∴将A与B坐标代入抛物线解析式得：

4a+4+c=5 a-2+c=-4

，
解得：

a=1 c=-3

，
故抛物线解析式为y=x²+2x-3=（x+1）²-4，
则它是由抛物线y=x²向左平移1个单位，向下平移4个单位得到的．

点评：此题考查了利用待定系数法确定二次函数解析式，平移规律，以及一元一次不等式的解法，待定系数法是数学中重要的思想方法，做题注意灵活运用．