Question

（2012•太原二模）如图，点A在反比例函数y=

4

x

(x＞0)的图象上，点B在反比例函数y=-

9

x

(x＜0)的图象上，且∠AOB=90°，则tan∠OAB的值为

3

2

．

Answer 1

分析：首先过点A作AC⊥x轴于C，过点B作BD⊥x轴于D，易得△OBD∽△AOC，又由点A在反比例函数y=

4

x

(x＞0)的图象上，点B在反比例函数y=-

9

x

(x＜0)的图象上，即可得S_△OBD=4.5，S_△AOC=2，然后根据相似三角形面积的比等于相似比的平方，即可得

OB

OA

=

3

2

，然后由正切函数的定义求得答案．

解答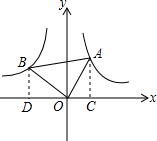：解：过点A作AC⊥x轴于C，过点B作BD⊥x轴于D，
∴∠ACO=∠ODB=90°，
∴∠OBD+∠BOD=90°，
∵∠AOB=90°，
∴∠BOD+∠AOC=90°，
∴∠OBD=∠AOC，
∴△OBD∽△AOC，
∴

S△OBD

S△AOC

=(

OB

OA

)2，
∵点A在反比例函数y=

4

x

(x＞0)的图象上，点B在反比例函数y=-

9

x

(x＜0)的图象上，
∴S_△OBD=4.5，S_△AOC=2，
∴

OB

OA

=

3

2

，
∴tan∠OAB=

OB

OA

=

3

2

．
故答案为：

3

2

．

点评：此题考查了相似三角形的判定与性质、反比例函数的性质以及直角三角形的性质．此题难度适中，注意掌握数形结合思想的应用，注意掌握辅助线的作法．