题目内容
(2012•太原二模)将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”,“面线”被这个平面图形截得的线段叫做该图形的“面径”,例如圆的直径就是它的“面径”.已知等边三角形的边长为2,则它的“面径”长可以是
,
(或介于
和
之间的任意两个实数)
,
(或介于
和
之间的任意两个实数)(写出2个).
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
分析:根据等边三角形的性质,最短的面径平行于三角形一边,最长的面径为等边三角形的高,然后根据相似三角形面积的比等于相似比的平方求出最短面径,根据等边三角形的性质求出高线,然后写出即可.
解答: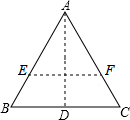 解:如图,EF∥BC时,EF为最短面径,
解:如图,EF∥BC时,EF为最短面径,
此时,(
)2=
,
即
=
,
解得EF=
,
等边三角形的高AD是最长的面径,
AD=
×2=
,
所以,它的面径长可以是
,
(或介于
和
之间的任意两个实数).
故答案为:
,
(或介于
和
之间的任意两个实数).
 解:如图,EF∥BC时,EF为最短面径,
解:如图,EF∥BC时,EF为最短面径,此时,(
| EF |
| BC |
| 1 |
| 2 |
即
| EF |
| 2 |
| ||
| 2 |
解得EF=
| 2 |
等边三角形的高AD是最长的面径,
AD=
| ||
| 2 |
| 3 |
所以,它的面径长可以是
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查了等边三角形的性质,读懂题意,弄明白面径的定义,并准确判断出等边三角形的最短与最长的面径是解题的关键.

练习册系列答案
相关题目
 (2012•太原二模)如图,点A在反比例函数
(2012•太原二模)如图,点A在反比例函数 (2012•太原二模)把一块直角三角板和一把直尺按如图所示的位置放在一起,测得∠2=35°,则∠1的度数是( )
(2012•太原二模)把一块直角三角板和一把直尺按如图所示的位置放在一起,测得∠2=35°,则∠1的度数是( )