题目内容
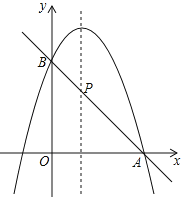
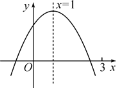
【题目】二次函数y＝ax2＋bx＋c(a≠0)图象如图所示，下列结论：①abc>0；②2a＋b＝0；③当m≠1时，a＋b>am2＋bm；④a－b＋c>0；⑤若a
＋bx1＝a
＋bx2且x1≠x2，则x1＋x2＝2，其中正确的有( )
A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
【答案】D
【解析】
根据抛物线开口方向得a＜0，由抛物线对称轴为直线x
1，得到b＝﹣2a＞0，即2a+b＝0，由抛物线与y轴的交点位置得到c＞0，所以abc＜0；根据二次函数的性质得当x＝1时，函数有最大值a+b+c，则当m≠1时，a+b+c＞am2+bm+c，即a+b＞am2+bm；根据抛物线的对称性得到抛物线与x轴的另一个交点在（﹣1，0）的右侧，则当x＝﹣1时，y＜0，所以a﹣b+c＜0；把ax12+bx1＝ax22+bx2先移项，再分解因式得到（x1﹣x2）[a（x1+x2）+b]＝0，而x1≠x2，则a（x1+x2）+b＝0，即x1+x2
，然后把b＝﹣2a代入计算得到x1+x2＝2．
∵抛物线开口向下，∴a＜0．
∵抛物线对称轴为直线x1，∴b＝﹣2a＞0，即2a+b＝0，所以②正确；
∵抛物线与y轴的交点在x轴上方，∴c＞0，∴abc＜0，所以①错误；
∵抛物线对称轴为直线x＝1，∴函数的最大值为a+b+c，∴当m≠1时，a+b+c＞am2+bm+c，即a+b＞am2+bm，所以③正确；
∵抛物线与x轴的一个交点在（3，0）的左侧，而对称轴为直线x＝1，∴抛物线与x轴的另一个交点在（﹣1，0）的右侧，∴当x＝﹣1时，y＜0，∴a﹣b+c＜0，所以④错误；
∵ax12+bx1＝ax22+bx2，∴ax12+bx1﹣ax22﹣bx2＝0，∴a（x1+x2）（x1﹣x2）+b（x1﹣x2）＝0，∴（x1﹣x2）[a（x1+x2）+b]＝0，而x1≠x2，∴a（x1+x2）+b＝0，即x1+x2．
∵b＝﹣2a，∴x1+x2＝2，所以⑤正确．
故选D．
【题目】某商场销售一种商品，进价为每个20元，规定每个商品售价不低于进价，且不高于60元，经调查发现，每天的销售量y（个）与每个商品的售价x（元）满足一次函数关系，其部分数据如下所示：
每个商品的售价x（元） | … | 30 | 40 | 50 | … |
每天的销售量y（个） | 100 | 80 | 60 | … |
（1）求y与x之间的函数表达式；
（2）设商场每天获得的总利润为w（元），求w与x之间的函数表达式；
（3）不考虑其他因素，当商品的售价为多少元时，商场每天获得的总利润最大，最大利润是多少？
