题目内容
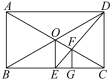
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC于E点,连接DE交OC于F点,作FG⊥BC于G点,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出相似比;若不是,请说明理由.
【答案】△ABC与△FGC是位似图形,位似中心是点C,△ABC与△FGC的相似比为3∶1.
【解析】
利用位似图形的性质得出位似中心,进而利用平行线分线段成比例定理求出即可;
△ABC与△FGC是位似图形,位似中心是点C.
因为在矩形ABCD中,AD∥BC,
所以∠FAD=∠FCE,∠FDA=∠FEC,
所以△AFD∽△CFE,
所以![]()
因为AD=BC,
所以![]()
因为∠ABC=90°,OE⊥BC,
所以OE∥AB.
因为OA=OC,
所以CE=![]() BC,
BC,
所以![]() =
=![]()
所以![]() =
=![]() .
.
即△ABC与△FGC的相似比为3∶1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】(本题8分)某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
1 | 2 | 3 | 4 | 5 | 6 | |
李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
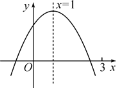
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.