题目内容
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化。开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分):
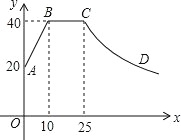
(1)分别求出线段AB和曲线CD的函数关系式;
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
【答案】(1)①![]() ;②
;②![]() ;(2)能
;(2)能
【解析】
(1)用代定系数法分别求出AB和CD的函数表达式
(2)分别求出注意力指数为36时的两个时间,再将两时间之差和19比较,大于19则能讲完,否则不能.
解:(1)设线段AB所在的直线的解析式为y1=k1x+20,
把B(10,40)代入得,k1=2,
∴y1=2x+20.
设C、D所在双曲线的解析式为y2=![]() ,
,
把C(25,40)代入得,k2=1000,
∴y2=![]()
(2)令y1=36,
∴36=2x+20,
∴x1=8
令y2=36,
∴36=![]() ,
,
∴x2=![]() ≈27.8
≈27.8
∵27.8-8=19.8>19,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】(本题8分)某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
1 | 2 | 3 | 4 | 5 | 6 | |
李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.