题目内容
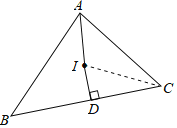
【题目】如图，I点为△ABC的内心，D点在BC上，且ID⊥BC，若∠B=44°，∠C=56°，则∠AID的度数为何？（ ）
A. 174 B. 176 C. 178 D. 180
【答案】A
【解析】
连接CI，利用三角形内角和定理可求出∠BAC的度数，由I点为△ABC的内心，可得出∠CAI、∠ACI、∠DCI的度数，利用三角形内角和定理可得出∠AIC、∠CID的度数，再由∠AID=∠AIC+∠CID即可求出∠AID的度数．
连接CI，如图所示．
在△ABC中，∠B=44°，∠ACB=56°，
∴∠BAC=180°﹣∠B﹣∠ACB=80°．
∵I点为△ABC的内心，
∴∠CAI=
∠BAC=40°，∠ACI=∠DCI=∠ACB=28°，
∴∠AIC=180°﹣∠CAI﹣∠ACI=112°，
又ID⊥BC，
∴∠CID=90°﹣∠DCI=62°，
∴∠AID=∠AIC+∠CID=112°+62°=174°．
故选：A．
练习册系列答案
相关题目
