题目内容
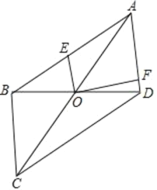
【题目】如图,在平行四边形ABCD中,对角线AC与BD相交于点O,AB=5,AD=3,E是AB上的一点,F是AD上的一点,连接BO和FO.
(1)当点E为AB中点时,求EO的长度;
(2)求线段AO的取值范围;
(3)当EO⊥FO时,连接EF.求证:BE+DF>EF.
【答案】(1)![]() ;(2)1<AO<4;(3)见解析.
;(2)1<AO<4;(3)见解析.
【解析】
(1) O是中点,E是中点,所以OE=![]() BC=
BC=![]() ;
;
(2) 在△ACD中利用三角形的第三边长小于两边之和,大于两边只差;
(3) 延长FO交BC于G点,就可以将BE,FD,EF放在一个三角形中,利用三角形两边之和大于第三边即可.
(1)解:∵四边形ABCD为平行四边形,
∴BC=AD=3,OA=OC,
∵点E为AB中点,
∴OE为△ABC的中位线,
∴OE=![]() BC=
BC=![]() ;
;
(2)解:在△ABC中,∵AB﹣BC<AC<AB+BC,
而OA=OC,
∴5﹣3<2AO<5+3,
∴1<AO<4;
(3)证明:延长FO交BC于G点,连接EG,如图,
∵四边形ABCD为平行四边形,
∴OB=OD,BC∥AD,
∴∠OBG=∠ODF,
在△OBG和△ODF中
 ,
,
∴△OBG≌△ODF,
∴BG=DF,OG=OF,
∵EO⊥OF,
∴EG=EF,
在△BEG中,BE+BG>EG,
∴BE+FD>EF.


练习册系列答案
相关题目