Question

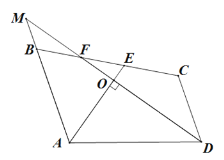
【题目】如图，等腰△ABC中，CA=CB=6，∠ACB=120°，点D在线段AB上运动（不与A、B重合），将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，给出下列结论：

①CD=CP=CQ；②∠PCQ为定值；③△PCQ面积的最小值为；④当点D在AB的中点时，△PDQ是等边三角形，其中正确结论的个数为（ ）

A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】C

【解析】①由折叠直接得到结论；②由折叠的性质求出∠ACP +∠BCQ=120°，再用周角的定义求出∠PCQ=120°；③先作出△PCQ的边PC上的高，用三角函数求出QE=CQ，得到S△PCQ =CD2，判断出△PCQ面积最小时，点D的位置，再求△PCQ面积的最小值即可；④先判断出△APD 是等边三角形，△BDQ是等边三角形，再求出∠PDQ=60°，即可得结论.

① ∵将△ CAD 与△ CBD 分别沿直线 CA、CB 翻折得到△CAP与△CBQ ，

∴CP=CD=CQ，

∴ ①正确；

② ∵将△ CAD与△CBD 分别沿直线CA、CB翻折得到△CAP 与△CBQ ，

∴∠ACP=∠ACD，∠BCQ=∠BCD ，

∴∠ACP +∠BCQ=∠ACD +∠BCD=∠ACB=120°，

∴∠ PCQ=360°﹣(∠ACP +BCQ +∠ACB ) =360°﹣(120°+120°) =120°，

∴∠ PCQ 的大小不变；

∴ ② 正确；

③ 如图，过点Q作QE ⊥ PC 交PC延长线于 E ，

∵∠PCQ=120°，

∴∠QCE=60°，

在 Rt△QCE 中， sin∠QCE=，

∴QE=CQ×sin∠QCE=CQ×sin60°=CQ ，

∵CP=CD=CQ，

∴ S△PCQ =×CP×QE=CP×CQ=CD 2，

∴ CD 最短时，S △ PCQ最小，

即:CD ⊥ AB 时，CD最短，

过点 C 作 CF ⊥ AB，此时 CF 就是最短的 CD ，

∵ AC=BC=6，∠ ACB=120°,

∴∠ ABC=30°，

∴CF=BC=3，

即:CD最短为3，

∴ S △ PCQ最小 =，

∴ ③错误；

④ ∵将△CAD与△CBD 分别沿直线CA、CB翻折得到△CAP与△CBQ ，

∴ AD=AP，∠ DAC=∠ PAC，

∵∠ DAC=30°，

∴∠ APD=60°，

∴△ APD是等边三角形，

∴ PD=AD，∠ ADP=60°，

同理：△ BDQ是等边三角形，

∴ DQ=BD，∠ BDQ=60°，

∴∠ PDQ=60°，

∵当点D在AB的中点，

∴AD=BD，

∴PD=DQ，

∴△DPQ 是等边三角形.

∴ ④正确.

正确的答案为：①②④ .

故选C.