题目内容
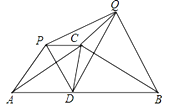
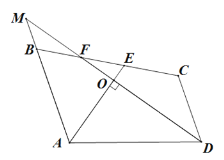
【题目】如图,四边形 ABCD 中,AE,DF 分别是∠BAD,∠ADC 的平分线,且 AE⊥DF 于点 O . 延长 DF 交 AB 的延长线于点 M .
(1)求证:AB∥DC ;
(2)若∠MBC=120°,∠BAD=108°,求∠C,∠DFE 的度数.
【答案】(1)见详解;(2)∠C=120°,∠DFE=24°
【解析】
(1)根据角平分线的定义可得∠DAB=2∠EAB,∠ADC=2∠ADF,根据垂直的定义可得∠AOD=90°,即∠DAE+∠ADF=90°,从而可得∠BAD+∠ADC=2(∠DAE+∠ADF)=180°,即可得证;
(2)由AB∥DC可得∠C=∠MBC,从而得出∠ADC=72°,再根据角平分线的定义以及三角形内角和公式解答即可.
解:(1)证明:∵AE,DF分别是∠BAD,∠ADC的平分线,
∴∠DAB=2∠EAB,∠ADC=2∠ADF,
∵AE⊥DF,
∴∠AOD=90°.
∴∠DAE+∠ADF=90°,
∴∠BAD+∠ADC=2(∠DAE+∠ADF)=180°,
∴AB∥DC;
(2)∵AB∥DC,
∴∠C=∠MBC.
∵∠MBC=120°,
∴∠C=120°,
∵∠BAD=108°,
∴∠ADC=72°,
∴![]() ,
,
∴∠DFE=180°﹣(∠C+∠CDF)=24°.

【题目】某教研机构为了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查.依据相关数据绘制成如图所示的不完整的统计图表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表

类别 | 人数 | 占总人数比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | c |
说不清楚 | 9 | 0.06 |
(1)求样本容量及表格中a,b,c的值,并补全统计图.
(2)若该校共有初中生2 300名,请估计该校“不重视阅读数学教科书”的初中生人数.
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?