题目内容
先阅读下面例题的解题过程,再解答后面的题目.
例题:解方程 (x2-1)2-5(x2-1)+4=0
我们可以将x2-1视为一个整体,然后设y=x2-1,则 (x2-1)2=y2,原方程转化为y2-5y+4=0.解得y1=1,y2=4.
当y=1时,x2-1=1,所以x=±
;当y=4时,x2-1=4,所以x=±
.
∴原方程的解为:x1=
,x2=-
,x3=
,x4=-
.
题目:用类似的方法试解方程(x2+x)2+(x2+x)=6.
例题:解方程 (x2-1)2-5(x2-1)+4=0
我们可以将x2-1视为一个整体,然后设y=x2-1,则 (x2-1)2=y2,原方程转化为y2-5y+4=0.解得y1=1,y2=4.
当y=1时,x2-1=1,所以x=±
| 2 |
| 5 |
∴原方程的解为:x1=
| 2 |
| 2 |
| 5 |
| 5 |
题目:用类似的方法试解方程(x2+x)2+(x2+x)=6.
设x2+x=y,
则原方程化为y2+y-6=0,
解得:y1=-3,y2=2,
当y=-3时,x2+x=-3,
即x2+x+3=0,
△=12-4×1×3<0,方程没有实数根,
当y=2时,原方程化为:x2+x=2,
即x2+x-2=0,
解得:x1=-2,x2=-1,
所以原方程的解是x1=-2,x2=-1.
则原方程化为y2+y-6=0,
解得:y1=-3,y2=2,
当y=-3时,x2+x=-3,
即x2+x+3=0,
△=12-4×1×3<0,方程没有实数根,
当y=2时,原方程化为:x2+x=2,
即x2+x-2=0,
解得:x1=-2,x2=-1,
所以原方程的解是x1=-2,x2=-1.

练习册系列答案
相关题目
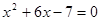 .
. 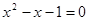
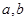 是方程
是方程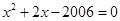 的两根,则
的两根,则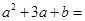 ()
()