题目内容
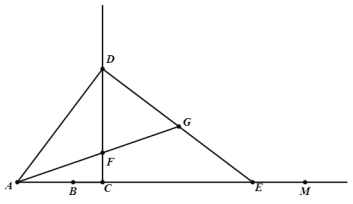
【题目】如图,已知△ABC.
(1)实践与操作:
利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)
①作BC边上的高AD;
②作△ABC的角平分线BE;
(2)综合与运用;
若△ABC中,AB=AC且∠CAB=36°,
请根据作图和已知写出符合括号内要求的正确结论;
结论1: ;(关于角)
结论2: ;(关于线段)
结论3: .(关于三角形)
【答案】(1)①②如图,见解析;(2)∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);BD=DC,AE=BE,BC=BE(关于线段);△ABE,△BCE都是等腰三角形(关于三角形).
【解析】
(1)①按照过直线外一点作直线的垂线步骤作即可;②按照作一个角的平分线的作法来做即可.
(2)根据等腰三角形的判定与性质结合(1)中的图形即可求解.
(1)①②如图:
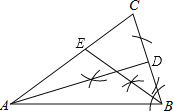
(2)∵AB=AC且∠CAB=36°,
∴∠ABC=∠C=72°,
∵BE是△ABC的角平分线,
∴∠ABE=∠CBE=36°,
∴∠ABE=∠CBE=∠CAB=36°.
∵AD是BC边上的高,AB=AC,
∴BD=DC,∠BAD=∠CAD.
∵∠EAB=∠ABE=36°,∠C=∠CEB=72°,
∴AE=BE,BC=BE,
∴△ABE,△BCE都是等腰三角形.
则结论1:∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);
结论2:BD=DC,AE=BE,BC=BE(关于线段);
结论3:△ABE,△BCE都是等腰三角形(关于三角形).
故答案为∠ABE=∠CBE=∠CAB=36°,∠BAD=∠CAD(关于角);BD=DC,AE=BE,BC=BE(关于线段);△ABE,△BCE都是等腰三角形(关于三角形).

练习册系列答案
相关题目