题目内容
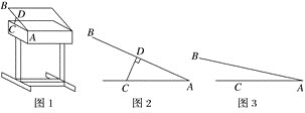
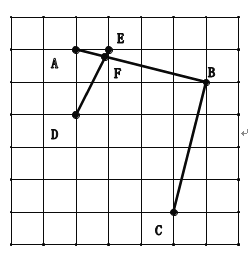
【题目】如图,在每个小正方形的边长为1的网格中,取格点A、B、C并连接AB,BC.取格点D、E并连接,交AB于点F.
(Ⅰ)BF的长等于_____;
(Ⅱ)若点G在线段BC上,且满足AF+CG=FG,请在如图所示的网格中,用无刻度的直尺,确定点G的位置,并简要说明点G的位置是如何找到的________________________________________(不要求证明).
【答案】(1)![]()
(2)见解析.
【解析】
(Ⅰ)先利用勾股定理计算AB,再利用相似三角形判定和性质计算即可.
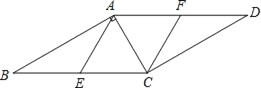
(Ⅱ)取格点M,连接AM,CM,得到正方形AMCB,取格点N,连接NM,EN,可得等腰直角三角形△EMN,∠EMN=45°,直线MN交BC于点G,点G即为所求.
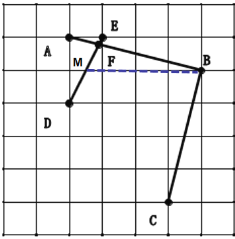
解:(Ⅰ)如图,设DE与网格线的交点为点M,点M是Rt△AED的斜边中点,所以MF=0.5, AB=![]() =
=![]() ,
,
∵AE∥BM
∴BF:AF=BM:AE=3.5:1=7:2,BF:AB=7:9,
∴BF= ![]() AB =
AB = ![]() .
.
(Ⅱ)如图,取格点M,连接AM,CM,得到正方形AMCB,取格点N,连接NM,EN,可得等腰直角三角形△EMN,∠EMN=45°,直线MN交BC于点G,点G即为所求.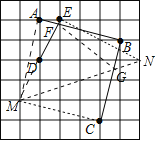

 浙江名校名师金卷系列答案
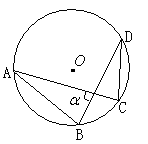
浙江名校名师金卷系列答案【题目】如图,Q是弧AB与弦AB所围成的图形的内部的一定点,P是弦AB上一动点,连接PQ并延长交弧AB于点C,连接BC.已知AB=6cm,设A,P两点间的距离为xcm,P,C两点间的距离为y1cm,A,C两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1,y2,随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)确定自变量x的取值范围是 .
(2)按下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值.
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.62 | 4.67 | 3.76 | 2.65 | 3.18 | 4.37 | |
y2/cm | 5.62 | 5.59 | 5.53 | 5.42 | 5.19 | 4.73 | 4.11 |
(3)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并面出函数y1,y2的图象.
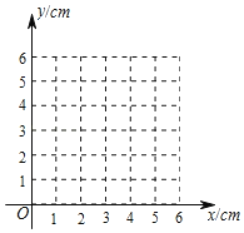
(4)结合函数图象,解决问题:当△APC为等腰三角形时,AP的长度约为 cm.