Question

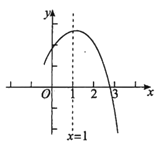
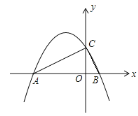
【题目】如图，二次函数y=ax2+bx+2的图象与x轴交于A、B两点，与y轴交于点C，若AC⊥BC，则a的值为_______．

Answer 1

【答案】

【解析】

根据c=2求得C点坐标为（0，2），则OC=2，设A（x1，0），B（x2，0），AC⊥BC，利用，求得OC2=OAOB，即4=|x1x2|=-x1x2；然后根据根与系数的关系列出方程，即可求得a的值．

解：设A（x1，0）（x1＜0），B（x2，0）（x2＞0），
∵当x=0时，y=2

∴C（0，2），∴OC=2

∵AC⊥BC，∴∠ACB＝90°

∴∠ACO+∠BCO＝90°

∵∠ACO+∠CAO＝90°
∴∠BCO＝∠CAO

∵∠AOC=∠COB＝90°

∴

∴

∴OC2=OAOB，即4=|x1x2|=-x1x2，
根据韦达定理知x1x2=，
∴a=-．
故答案为：-．