题目内容
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF;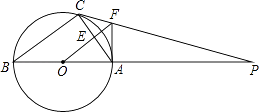
(1)判断AF与⊙O的位置关系并说明理由.
(2)若⊙O的半径为4,AF=3,求AC的长.
【答案】
(1)解:证明:连接OC,如图所示:

∵AB是⊙O直径,
∴∠BCA=90°,
∵OF∥BC,
∴∠AEO=90°,∠1=∠2,∠B=∠3,
∴OF⊥AC,
∵OC=OA,
∴∠B=∠1,
∴∠3=∠2,
在△OAF和△OCF中,
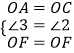 ,
,
∴△OAF≌△OCF(SAS),
∴∠OAF=∠OCF,
∵PC是⊙O的切线,
∴∠OCF=90°,
∴∠OAF=90°,
∴FA⊥OA,
∴AF是⊙O的切线;
(2)解:∵⊙O的半径为4,AF=3,∠OAF=90°,
∴OF= ![]() =
= ![]() =5
=5
∵FA⊥OA,OF⊥AC,
∴AC=2AE,△OAF的面积= ![]() AFOA=
AFOA= ![]() OFAE,
OFAE,
∴3×4=5×AE,
解得:AE= ![]() ,
,
∴AC=2AE= ![]() .
.
【解析】(1)要证切线可证垂直,由CF是切线须连接OC,得垂直,证出△OAF≌△OCF,得到∠OAF=∠OCF,由切线得∠OCF=90°,进而∠OAF=90度,证出切线;(2)由面积法先求出AE,进一步求出AC.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目