Question

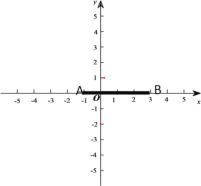
【题目】如图，方格纸中的每个小正方形的边长都为1，在建立平面直角坐标系后，△ABC的顶点均在格点上．

（1）以点A为旋转中心，将△ABC绕点A顺时针旋转90°得到△AB1C1，画出△AB1C1；

（2）画出△ABC关于原点O成中心对称的△A2B2C2，若点B的坐标为（-2，-2），则点B2的坐标为_________．

（3）若△A2B2C2可看作是由△AB1C1绕点P顺时针旋转90°得到的，则点P的坐标为______.

Answer 1

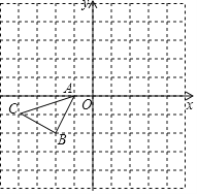
【答案】（1）见解析；（2）图见解析；（2，2）；（3）（0，-1）

【解析】

（1）利用网格特点和旋转的性质画出B、C的对应点B1、C1，从而得到△AB1C1．

（2）利用关于原点对称的点的坐标特征写出A2、B2、C2的坐标，然后描点连线即可；

（3）连接A1A2，C1C2，作A1A2和C1C2的垂直平分线交于点P，观察图形即可得出结论．

（1）如图，△AB1C1为所作；

（2）如图，△A2B2C2为所作；若点B的坐标为（-2，-2），则点B2的坐标为（2，2）；

（3）连接A1A2，C1C2，作A1A2和C1C2的垂直平分线交于点P，由图可知：P（0，-1）．