题目内容
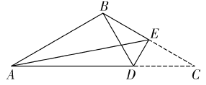
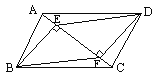
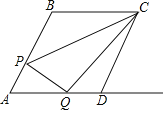
【题目】如图,在边长为1的菱形ABCD中,∠ABC=120°,P是边AB上的动点,过点P作PQ⊥AB交射线AD于点Q,连接CP,CQ,则△CPQ面积的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
设菱形的高为h,解直角三角形求得h=![]() ,设AP=x,则PB=1﹣x,AQ=2x,PQ=
,设AP=x,则PB=1﹣x,AQ=2x,PQ=![]() x,DQ=1﹣2x,然后根据S△CPQ=S菱形ABCD﹣S△PBC﹣S△PAQ﹣S△CDQ表示出△APQ的面积,根据二次函数的性质即可求得.
x,DQ=1﹣2x,然后根据S△CPQ=S菱形ABCD﹣S△PBC﹣S△PAQ﹣S△CDQ表示出△APQ的面积,根据二次函数的性质即可求得.
解:设菱形的高为h,
∵在边长为1的菱形ABCD中,∠ABC=120°,
∴∠A=60°,
∴h=![]() ,
,
若设AP=x,则PB=1﹣x,
∵PQ⊥AB,
AQ=2x,PQ=![]() x,
x,
∴DQ=1﹣2x,
∴S△CPQ=S菱形ABCD﹣S△PBC﹣S△PAQ﹣S△CDQ
=1×![]() ﹣
﹣![]() (1﹣x)
(1﹣x)![]() ﹣
﹣![]() x
x![]() x﹣
x﹣![]() (1﹣2x)
(1﹣2x)![]()
=﹣![]() x2+
x2+![]() x
x
=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴△CPQ面积有最大值为![]() ,
,
故选:D.

练习册系列答案
相关题目
【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
|
| m | ... |
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).