题目内容
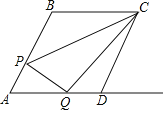
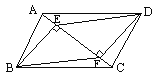
【题目】已知：如图，
ABCD中，E、F分别是AC上两点，且BE⊥AC于E，DF⊥AC于F．求证：四边形BEDF是平行四边形．
【答案】证明见解析.
【解析】试题分析：首先根据平行四边形的性质得出AB和CD平行且相等，从而得出∠BAE=∠DCF，然后根据垂直得出BE∥DF，∠BEA=∠DFC=90°，从而可以说明△ABE和△CDF全等，从而得出BE=DF，最后根据一组对边平行且相等的四边形为平行四边形得出答案.
试题解析：∵ 四边形ABCD是平行四边形， ∴ AB=CD 且AB∥CD
∴∠BAE=∠DCF． ∵ BE⊥AC于E DF⊥AC于F
∴ BE∥DF 且 ∠BEA=∠DFC=90°． ∴ △ABE≌△CDF （AAS）
∴ BE=DF ∴ 四边形BEDF是平行四边形（一组对边平行且相等的四边形平行四边形）
练习册系列答案
相关题目
【题目】某校为了了解全校学生寒假参加社区实践活动的情况，学校随机调查本校100名学生参加社区实践活动的次数，并将调查所得的数据整理如下：
参加社区实践活动次数的频数、频率分布表
活动次数 | 频数 | 频率 |
| 20 | 0..20 |
|
| 0.24 |
| 32 |
|
| 12 |
|
| 8 |
|
| 4 |
|
参加社区实践活动次数的频数分布直方图
根据以上图表信息，解答下列问题．
（1）表中
______，
_______．
（2）若频数分布直方图中，从左到右依次为第一组，第二组，……，第六组，那么样本数据的中位数落在第________组．
（3）请把频数分布直方图补充完整（画图后请标注相应的数据）．
（4）若该校共有1200名学生，请估计这个寒假该校参加社区活动超过6次的学生有多少人？
