题目内容
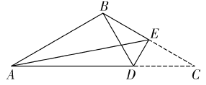
【题目】如图，在等腰三角形纸片
中，
，点
分别在边
上，连接
，将
沿翻折使得点
恰好落在点
处，则
的长为（ ）
A.
B.
C.
D.
【答案】C
【解析】
过点E作EH⊥AB，交AB的延长线于点H，由等腰△ABC，点C与点B关于直线DE对称，可以推出BE=CE=
BC，在Rt△BEH中，∠EBH=60°，利用三角函数求得EH、BH，然后由勾股定理求出AE即可．
过点E作EH⊥AB，交AB的延长线于点H，如图，
∴∠H=90°，
∵△ABC是等腰三角形，∠ABC=120°，
∴AB=BC=6，
∵点C与点B关于直线DE对称，
∴BE=CE=BC=×6=3，
在Rt△BEH中，∠EBH=180°-∠ABC=180°-120°=60°，
∴BH=BE
=3cos60°=3×=
，
EH=BE
=3sin60°=3×
=
，
∴AH=AB+BH=6+
，
在Rt△AEH中，AE=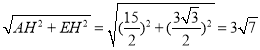
，
故选：C．
【题目】为了让学生掌握知识更加牢固，某校九年级物理组老师们将物理实验的教学方式由之前的理论教学改进为理论+实践，一段时间后，从九年级随机抽取15名学生，对他们在教学方式改进前后的物理实验成绩（百分制）进行整理、描述和分析（成绩用
表示，共分成4组：A．
，B．
，C．
，D．
），下面给出部分信息：
教学方式改进前抽取的学生的成绩在
组中的数据为：80，83，85，87，89．
教学方式改进后抽取的学生成绩为：72，70，76，100，98，100，82，86，95，90，100，86，84，93，88．
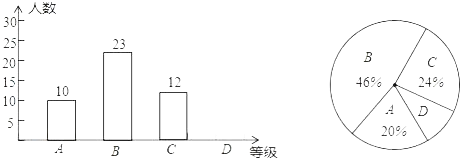
教学方式改进前抽取的学生成绩频数分布直方图
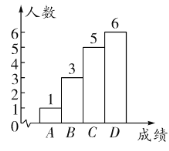
教学方式改进前后抽取的学生成绩对比统计表
统计量 | 改进前 | 改进后 |
平均数 | 88 | 88 |
中位数 |
|
|
众数 | 98 |
|
根据以上信息，解答下列问题：
（1）直接写出上述图表中
的值；
（2）根据以上数据，你认为该校九年级学生的物理实验成绩在教学方式改进前好，还是改进后好？请说明理由（一条理由即可）；
（3）若该校九年级有300名学生，规定物理实验成绩在90分及以上为优秀，估计教学方式改进后成绩为优秀的学生人数是多少？
