题目内容
【题目】说明:在解答“结论应用”时,从(A),(B)两题中仸选一题做答.
问题探究
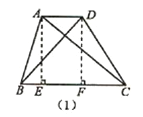
启知学习小组在课外学习时,发现了这样一个问题:如图(1),在四边形ABCD中,连接AC,BD,如果△ABC与△BCD的面积相等,那么AD∥BC.在小组交流时,他们在图(1)中添加了如图所示的辅助线,AE⊥BC于点E,DF⊥BC于点F.请你完成他们的证明过程.
结论应用
在平面直角坐标系中,反比例函数![]() 的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
(A)(1)求反比例函数的表达式;
(2)如图(2),已知b=1,AC,BD相交于点E,求证:CD∥AB.
(B)(1)求反比例函数的表达式;
(2)如图(3),若点B在第三象限,判断并证明CD与AB的位置关系.
我选择:


【答案】问题探究:证明见解析证明;结论应用:若选(A)(1)![]() ;(2)见解析证明;若选(B)(1)
;(2)见解析证明;若选(B)(1)![]() ;(2)CD∥AB,见解析证明.
;(2)CD∥AB,见解析证明.
【解析】
试题分析:问题探究:根据![]()
![]() ,可得AE=DF,根据AE⊥BC,DF⊥BC,得AE∥DF,所以可判定四边形AEFD是平行四边形,即可得出结论;
,可得AE=DF,根据AE⊥BC,DF⊥BC,得AE∥DF,所以可判定四边形AEFD是平行四边形,即可得出结论;
结论应用:若选(A)(1)把A点的坐标代入解析式即可求出m的值即可;(2)连接AD、BC,将b=1代入函数表达式得a=4,由C、D、E三点的坐标可知CE=DE=1,AE=BE=3,进而可得![]()
![]() ,即可得出结论;
,即可得出结论;
若选(B)(1)把A点的坐标代入解析式中即可求出m的值即可;(2)连接AD、BC,延长BD,AC相交于点M,由题意得M点坐标为(1,b),BM=1-a,AM=4-b,且![]() ,通过计算可得出
,通过计算可得出![]()
![]() ,即可得出结论.
,即可得出结论.
试题解析:问题探究:∵![]() ,
,![]() ,∵
,∵![]()
![]() ,∴AE=DF,又∵AE⊥BC,DF⊥BC,∴AE∥DF,∴四边形AEFD是平行四边形,∴AD∥BC;
,∴AE=DF,又∵AE⊥BC,DF⊥BC,∴AE∥DF,∴四边形AEFD是平行四边形,∴AD∥BC;
结论应用:若选(A)(1)把A点的坐标代入解析式中得:4=![]() ,m=4,∴反比例函数的表达式为:
,m=4,∴反比例函数的表达式为:![]() ;
;
(2)连接AD、BC,将b=1代入函数表达式得:a=4,又∵AC⊥x,BD⊥y,∴AC⊥BD,C(1,0),D(0,1),E(1,1),∴CE=DE=1,AE=BE=3,又∵![]() ,∴
,∴![]() 且AC=BD=4,BE=AE=3,∴
且AC=BD=4,BE=AE=3,∴![]()
![]() ,∴CD∥AB;
,∴CD∥AB;

若选(B)(1)把A点的坐标代入解析式中得:4=![]() ,m=4,∴反比例函数的表达式为:
,m=4,∴反比例函数的表达式为:![]() ;
;
(2)CD∥AB,证明如下:连接AD、BC,延长BD,AC相交于点M,由题意得M点坐标为(1,b),BM=1-a,AM=4-b,且![]() ,∴
,∴![]() =
=![]() ×4(1-a)=2(1-a),
×4(1-a)=2(1-a),![]() =
=![]() (-a)(4-b)=
(-a)(4-b)=![]() (-a)(4-
(-a)(4-![]() )=2(1-a),∴
)=2(1-a),∴![]()
![]() ,∴CD∥AB.
,∴CD∥AB.


 名校课堂系列答案
名校课堂系列答案