题目内容
 如图,在?ABCD中,E是AD的中点,CE的延长线交BA的延长线于点F.
如图,在?ABCD中,E是AD的中点,CE的延长线交BA的延长线于点F.
(1)求证:CD=AF;
(2)连接BE,且BE⊥CF,则CD与BC之间的长度关系是什么,并说明理由.
解:(1)证明:∵E是AD的中点,
∴AE=DE.
在△FAE和△CDE中,
∠FEA=∠CED,AE=DE,∠D=∠A,
∴△FAE≌△CDE.
∴CD=AF.
(2)BC=2CD.
∵CD=AF,AB=CD,
∴AF+AB=BF=2CD.
∵BE⊥CF,
∴∠BEF=∠BEC,
∵CE=FE,BE=BE,
∴△BEF≌△BEC.
∴BF=BC.
∴BC=2CD.
分析:(1)因为E是AD的中点,所以AE=DE,又因为∠FEA=∠CED,则可根据ASA判定△FAE≌△CDE,即CD=AF;
(2)因为CE=FE,BE⊥CF,BE共边,所以△BEF≌△BEC,则BF=BC,又因为CD=AF,AB=CD,所以BF=2CD,即BC=2CD.
点评:本题把全等三角形的判定和性质结合求解.有利于培养学生综合运用数学知识的能力.
∴AE=DE.
在△FAE和△CDE中,
∠FEA=∠CED,AE=DE,∠D=∠A,
∴△FAE≌△CDE.
∴CD=AF.
(2)BC=2CD.
∵CD=AF,AB=CD,
∴AF+AB=BF=2CD.
∵BE⊥CF,
∴∠BEF=∠BEC,
∵CE=FE,BE=BE,
∴△BEF≌△BEC.
∴BF=BC.
∴BC=2CD.
分析:(1)因为E是AD的中点,所以AE=DE,又因为∠FEA=∠CED,则可根据ASA判定△FAE≌△CDE,即CD=AF;
(2)因为CE=FE,BE⊥CF,BE共边,所以△BEF≌△BEC,则BF=BC,又因为CD=AF,AB=CD,所以BF=2CD,即BC=2CD.
点评:本题把全等三角形的判定和性质结合求解.有利于培养学生综合运用数学知识的能力.

练习册系列答案
相关题目
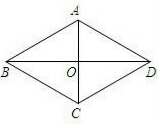 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=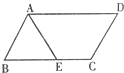 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
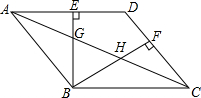
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.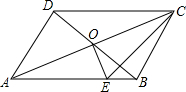 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是