题目内容
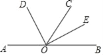
【题目】如图,点A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)写出图中所有互为余角的角.
【答案】(1)90°;(2)见解析.
【解析】
(1)根据邻补角定义得∠AOC+∠BOC=180°,由角平分线定义得∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,所以∠COD+∠COE=
∠BOC,所以∠COD+∠COE=![]() (∠AOC+∠BOC)=90°.即∠DOE=90°.
(∠AOC+∠BOC)=90°.即∠DOE=90°.
(2)根据(1)的结论,可以得到互余的角.
解:(1)∵点A,O,B在同一条直线上,
∴∠AOC+∠BOC=180°,
∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC
∠BOC
∴∠COD+∠COE=![]() (∠AOC+∠BOC)=90°,
(∠AOC+∠BOC)=90°,
∴∠DOE=90°;
(2)互为余角的角有:
∠COD和∠COE,∠AOD和∠BOE,∠AOD和∠COE,∠COD和∠BOE.

练习册系列答案
相关题目