题目内容
【题目】如图，已知⊙O的半径长为R=5，弦AB 与弦CD平行，他们之间距离为7，AB=6求：弦CD的长．
【答案】过O向AB作垂线，垂足为E ， 根据垂径定理可以得到AE=3，连接OA ， 在直角三角形AOE中，根据勾股定理可以得到OE= 
.同样过O点想CD作垂线，垂足为F ， 因为弦AB和弦CD之间的距离为7，那么OF=3，连接OC ， 在直角三角形OCF中CF= ，根据垂径定理可以知道点F为CD的中点，即CD=8.
【解析】此题考查了垂径定理和勾股定理知识点.
【考点精析】通过灵活运用勾股定理的概念和垂径定理，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧即可以解答此题．
鸿图图书寒假作业假期作业吉林大学出版社系列答案
【题目】水产公司有一种海产品共2 104千克，为寻求合适的销售价格，进行了8天试销，试销情况如下：
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | 第8天 | |
售价x(元/千克) | 400 | 250 | 240 | 200 | 150 | 125 | 120 | |
销售量y(千克) | 30 | 40 | 48 | 60 | 80 | 96 | 100 |
观察表中数据，发现可以用反比例函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系．现假定在这批海产品的销售中，每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系．
（1）写出这个反比例函数的解析式，并补全表格；
（2）在试销8天后，公司决定将这种海产品的销售价格定为150元/千克，并且每天都按这个价格销售，那么余下的这些海产品预计再用多少天可以全部售出？
（3）在按（2）中定价继续销售15天后，公司发现剩余的这些海产品必须在不超过2天内全部售出，此时需要重新确定一个销售价格，使后面两天都按新的价格销售，那么新确定的价格最高不超过每千克多少元才能完成销售任务？
【答案】（1）
，表格中填：300，50；（2）20天（3）最高不超过每千克60元。.
【解析】整体分析：
（1）根表格中x，y的对应值确定x，y的函数关系式，补全表格；（2）分别求出8天后剩余的产品数量及第8天的产品价格；（3）确定继续销售15天后的产品数量，求出后2天每天的销售量，即可求解.
（1）∵xy=12000，
∴反比例函数的解析式y＝
.
当y=40时，x=
=300；
当x=240时y=
=50.
（2）销售8天后剩下的数量2104-（30+40+48+50+60+80+96+100）=1600，
当x=150时，y＝
=80，
∴1600÷80=20天，
∴余下的这些海产品预计再用20天可以全部售出．
（3）1600-80×15=400千克，
400÷2=200千克/天，
即如果正好用2天售完，那么每天需要售出200千克．
当y=200时，x＝
=60.
所以新确定的价格最高不超过60元/千克才能完成销售任务．
【题型】解答题
【结束】
22
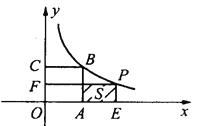
【题目】如图,已知正方形
的面积为9，点
为坐标原点，点
在
轴上，点
在
轴上，点
在函数
的图象上，点
为其双曲线上的任一点，过点
分别作
轴、
轴的垂线，垂足分别为
、
，并设矩形
和正方形
不重合部分的面积为
．
（1）求
点坐标和
的值；
（2）当
时，求
点坐标；
（3）写出
关于
的函数关系式．
