题目内容
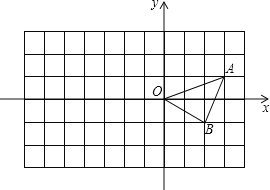
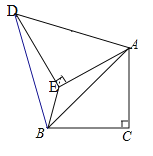
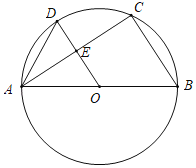
【题目】如图,AB是⊙O的直径,C、D是⊙O上的两点,且OD∥BC,OD与AC交于点E,连接AD.
(1)求证:AE=CE;
(2)若∠B=60°,求∠CAD的度数;
(3)若AC=4,BC=3,求DE的长.
【答案】(1)证明见解析;(2)30°;(3)1.
【解析】
(1)由相似三角形的判定与性质,线段和差证明得AE=CE;
(2)由圆周角定理,平行线性质,等腰三角形的判定与性质,角的和差求出∠CAD的度数为30°;
(3)由勾股定理,相似三角形的性质,线段的和差,等量代换求出DE的长为1.
(1)如图所示:
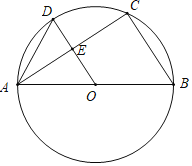
∵OD∥BC,
∴△AOE∽△ABC,
∴![]() ,
,
又∵AB是⊙O的直径,
∴AB=2AO,
∴![]() ,
,
又∵AC=AE+EC,
∴AE=EC;
(2)∵AB是⊙O的直径,
∴∠ACD=90°,
又∵OD∥BC,
∴∠B=∠ACE,∠ACD=∠AED,
又∴∠B=60°,
∴∠AOE=60°,∠AEO=90°,
又∵∠EAO+∠AOE=90°,
∴∠EAO=30°,
又∵AO=DO,
∴∠OAD=60°,
又∵∠OAD=∠OAE+∠CAD,
∴∠CAD=60°﹣30°=30°;
(3)在Rt△ACB中,由勾股定理得:
![]() =
=![]() =5,
=5,
∴OA=![]() ,
,
∴OD=![]() ,
,
又∵![]() ,BC=3,
,BC=3,
∴OE=![]() ,
,
又∵OD=OE+DE,
∴DE=![]() =1.
=1.

练习册系列答案
相关题目