题目内容
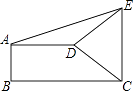
【题目】在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.
(1)如图1,①∠BEC=_________°;
②在图1已有的三角形中,找到一对全等的三角形,并证明你的结论;
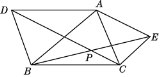
(2)如图2,FH∥CD交AD于点H,交BE于点M.NH∥BE,NB∥HE,连接NE.若AB=4,AH=2,求NE的长.

图1 图2
【答案】45
【解析】
(1)根据矩形的性质得到![]() ,根据角平分线的定义得到
,根据角平分线的定义得到![]() ,根据三角形内角和定理计算即可;
,根据三角形内角和定理计算即可;
(2)利用![]() 定理证明
定理证明![]() ;
;
(3)连接![]() ,证明四边形
,证明四边形![]() 是矩形,得到
是矩形,得到![]() ,根据勾股定理求出
,根据勾股定理求出![]() 即可.
即可.
(1)①∵四边形ABCD为矩形,
∴∠ABC=∠BCD=90°,
∵BE平分∠ABC,
∴∠EBC=45°,
∴∠BEC=45°,
故答案为:45;
②△ADE≌△ECF,
理由如下:∵四边形ABCD是矩形,
∴∠ABC=∠C=∠D=90°,AD=BC.
∵FE⊥AE,
∴∠AEF=90°.
∴∠AED+∠FEC=180°-∠AEF=90°.
∵∠AED+∠DAE=90°,
∴∠FEC=∠EAD,
∵BE平分∠ABC,
![]()
∴∠BEC=45°.
∴∠EBC=∠BEC.
∴BC=EC.
∴AD=EC.
在△ADE和△ECF中,
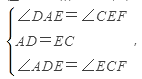
∴△ADE≌△ECF;
(2)连接HB,如图2,
∵FH∥CD,
∴∠HFC=180°-∠C=90°.
∴四边形HFCD是矩形.
∴DH=CF,
∵△ADE≌△ECF,
∴DE=CF.
∴DH=DE.
∴∠DHE=∠DEH=45°.
∵∠BEC=45°,
∴∠HEB=180°-∠DEH-∠BEC=90°.
∵NH∥BE,NB∥HE,
∴四边形NBEH是平行四边形.
∴四边形NBEH是矩形.
∴NE=BH.
∵四边形ABCD是矩形,
∴∠BAH=90°.
∵在Rt△BAH中,AB=4,AH=2,
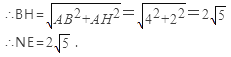

 名校课堂系列答案
名校课堂系列答案【题目】某校要从甲、乙、丙、丁四名学生中选一名参加“汉字听写”大赛,选拔中每名学生的平均成绩 ![]() 及其方差s2如表所示,如果要选拔一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
及其方差s2如表所示,如果要选拔一名成绩高且发挥稳定的学生参赛,则应选择的学生是( )
甲 | 乙 | 丙 | 丁 | |
| 8.9 | 9.5 | 9.5 | 8.9 |
s2 | 0.92 | 0.92 | 1.01 | 1.03 |
A.甲
B.乙
C.丙
D.丁