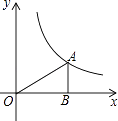��Ŀ����
����Ŀ���Ķ����⣺
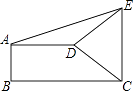
��ͼ������ƽ��ֱ������ϵ�У�����֪��A��xA��yA���͵�C��xC��yC������MΪ�߶�AC���е㣬����������ȫ�ȵ�֪ʶ������AMP�ա�CMQ������PM=MQ��PA=QC����xM��xA=xC��xM��yA��yM=yM��yC���Ӷ��� �����е�M������Ϊ��
�����е�M������Ϊ��![]() ��
��![]() ����
����

����֪ʶ��
��1����ͼ������A��C�������ֱ�A����1��3����C��3����1������AC�е�M�����ꣻ
����������
��2����ͼ������ƽ��ֱ������ϵ�У�ABCD�Ķ���A��B��C������ֱ�Ϊ����1��5��������2��2������3��3�������D�����ꣻ
��3����ͼ������A�Ƿ���������y=![]() ��x��0���ϵĶ��㣬����A��AB��x�ᣬAC��y�ᣬ�ֱ���y�T
��x��0���ϵĶ��㣬����A��AB��x�ᣬAC��y�ᣬ�ֱ���y�T![]() ��x��0����ͼ���ڵ�B��C����D��ֱ��y=2x�ϵĶ��㣬��̽���ڵ�A�˶������У���A��B��C��DΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ������ʱ��A�����ꣻ�����ܣ���˵�����ɣ�
��x��0����ͼ���ڵ�B��C����D��ֱ��y=2x�ϵĶ��㣬��̽���ڵ�A�˶������У���A��B��C��DΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ������ʱ��A�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1����1��1������2����4��6������3����A������Ϊ��2![]() ��
��![]() ������
������![]() ��4
��4![]() ������2��4��
������2��4��
��������
��1�������߶ε��е����깫ʽ���ɵô𰸣�
��2������ƽ���ı��εĶԽ�����ƽ�֣��ɵ�M��AC���е㣬M��BD���е㣬�����е����깫ʽ���ɵô𰸣�
��3������ƽ���ı��ζԽǵĶ���ĺ�����ĺ���ȣ�������ĺ���ȣ��ɵõ�D�����꣬���ݵ��ں���ͼ���ϣ��ɵ�a��ֵ�����ݵ�A�������ǣ�a��![]() �����ɵõ�A�����꣮
�����ɵõ�A�����꣮
��1����A��C�����������е����깫ʽ����
xM=![]() =1��yM=
=1��yM=![]() =1��
=1��
AC�е�M�����꣨1��1����
��2������AC��BD���ڵ�M���ı���ABCD��ƽ���ı��Σ�
��M��AC��BD�Ľ��㣬
��A����1��5����C��3��3������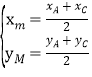 ��
��
���![]() ��
��
����M��������1��4����
���D��������xD��yD����
���е����깫ʽ����
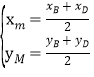 ��
��
���![]() ��
��
����D��������4��6����
��3����A��a��![]() ������B��
������B��![]() ��
��![]() ��C��a��
��C��a��![]() ����
����
�ٵ�ABΪ�Խ���ʱ����![]() ��
��
��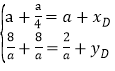 ��
��
���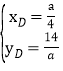 ��
��
��D��![]() ��
��![]() ������y=2x���a=2
������y=2x���a=2![]() ��
��
A��2![]() ��
��![]() ����
����
�ڵ�ACΪ�Խ���ʱ����![]() ��
��
��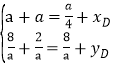
���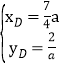
��D��![]() a��
a��![]() ������y=2x���a=
������y=2x���a=![]() ��
��
A��![]() ��4
��4![]() ����
����
�۵�ADΪ�Խ���ʱ����![]()
��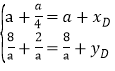 ��
��
���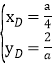
��D��![]() ��
��![]() ������y=2x���a=2��
������y=2x���a=2��
A��2��4����
������������A��������2![]() ��
��![]() ������
������![]() ��4
��4![]() ������2��4����
������2��4����

 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�