题目内容
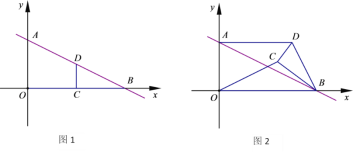
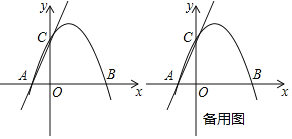
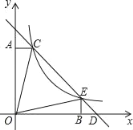
【题目】如图,直线y=﹣x+b与反比例函数y=![]() (k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACO=S△BEO;④S△CEO=15;⑤点D的坐标为(5,0).其中正确的是( )
(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACO=S△BEO;④S△CEO=15;⑤点D的坐标为(5,0).其中正确的是( )
A. ①②③B. ①②③④C. ②③④⑤D. ①②③⑤
【答案】D
【解析】
①只需把点C的坐标代入两个函数的解析式,就可得到k和b的值;②易证OD=OF,从而可得∠ODF=45°,即可证到△BED是等腰直角三角形;③只需求出点E的坐标,就可求出△ACD和△BED的面积;④只需根据点C、B、D的坐标就可求出△CBD的面积;⑤把yD=0代入直线的解析式,就可解决问题.
①∵直线y=﹣x+b与反比例函数y=![]() (k≠0)的图象的一支交于C(1,4),
(k≠0)的图象的一支交于C(1,4),
∴4=﹣1+b,k=xy=1×4=4,故①正确;
②∵点D、F分别是直线y=﹣x+5与x轴、y轴的交点,
∴点D的坐标为(5,0),点F的坐标为(0,5),
∴OD=OF=5.
∵∠DOF=90°,
∴∠ODF=45°.
∵EB⊥x轴,
∴△BED是等腰直角三角形,故②正确;
③∵反比例函数y=![]() ,
,
∴S△ACO=S△BEO=|4|=4,故③正确;
④解方程组 ,得
,得![]() 或
或![]() ,
,
∴E的坐标为(4,1),
∴△OCE的面积=△OCD的面积﹣△ODE的面积=![]() ×5×4﹣
×5×4﹣![]() ×5×1=
×5×1=![]() ,故④错误;
,故④错误;
⑤∵点D是直线y=﹣x+5与y轴的交点,
∴点D的坐标为(5,0),故⑤正确;
故选:D.

 阅读快车系列答案
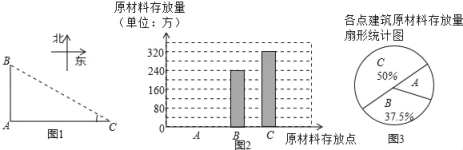
阅读快车系列答案【题目】重庆八中将于2017年整体搬迁至渝北空港新城,新校园工程建设正在如火如荼的进行.经工程部管理人员同意,四位同学前往工地进行社会实践活动.如图,A、B、C是三个建筑原材料存放点,点B、C分别位于点A的正北和正东方向,AC=400米.四人分别测得∠C的度数如表:
甲 | 乙 | 丙 | 丁 | |
∠C(单位:度) | 34 | 36 | 38 | 40 |
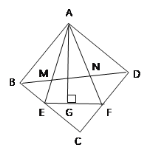
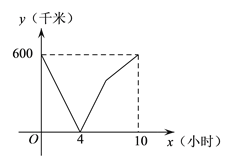
他们又调查了各点的建筑材料存放量,并绘制了下列尚不完整的统计如图、如图:
(1)求表中∠C度数的平均数![]() ;
;
(2)求A处的建筑原材料存放量,并将如图补充完整;
(3)用(1)中的![]() 作为∠C的度数,要将A处的全部建筑原材料沿道路AB运到B处,已知运1方建筑原材料每米的费用为0.1元,求运完全部建筑原材料所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
作为∠C的度数,要将A处的全部建筑原材料沿道路AB运到B处,已知运1方建筑原材料每米的费用为0.1元,求运完全部建筑原材料所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)