题目内容
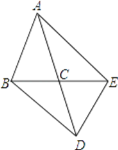
【题目】如图,在△ABC中,AB=AC,△ABC与△DEC关于点C成中心对称,连接AE、BD.
(1)线段AE、BD具有怎样的位置关系和大小关系?说明你的理由.
(2)如果△ABC的面积为5cm2 , 求四边形ABDE的面积.
(3)当∠ACB为多少度时,四边形ABDE为矩形?说明你的理由.
【答案】(1)见解析;(2)20cm2;(3)∠ACB=60°时,四边形ABDE为矩形, 理由见解析.
【解析】
(1)根据中心对称的性质可得AC=CD,BC=CE,然后根据对角线互相平分的四边形是平行四边形得到四边形ABDE是平行四边形,再根据平行四边形的对边互相平行且相等解答;
(2)根据平行四边形的性质,对角线把四边形分成面积相等的四个部分解答;
(3)∠ACB=60°.先判断出△ABC是等边三角形,根据等边三角形的三条边都相等可得AC=BC,然后求出AD=BE,再根据对角线相等的平行四边形是矩形证明.
(1)∵△ABC与△DEC关于点C成中心对称,
∴AC=CD,BC=CE,
∴四边形ABDE是平行四边形,
∴AE与BD平行且相等;
(2)∵四边形ABDE是平行四边形,
∴S△ABC=S△BCD=S△CDE=S△ACE,
∵△ABC的面积为5cm2,
∴四边形ABDE的面积=4×5=20cm2;
(3)∠ACB=60°时,四边形ABDE为矩形.
理由如下:∵AB=AC,∠ACB=60°,
∴△ABC是等边三角形,
∴AC=BC,
∵四边形ABDE是平行四边形,
∴AD=2AC,BE=2BC,
∴AD=BE,
∴四边形ABDE为矩形.

练习册系列答案
相关题目