题目内容
【题目】一、阅读理解:
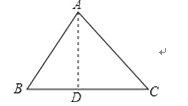
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则a2+b2=c2;
(2)若∠C为锐角,则a2+b2与c2的关系为:a2+b2>c2;
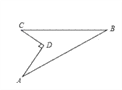
(3)若∠C为钝角,试推导a2+b2与c2的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c,若△ABC是钝角三角形,求第三边c的取值范围.
【答案】一、(1)a2+b2=c2;(2)a2+b2>c2;(3)a2+b2<c2;
二、5<c<7或1<c<![]() .
.
【解析】
试题分析:一、(1)由勾股定理即可得出结论;
(2)作AD⊥BC于D,则BD=BC﹣CD=a﹣CD,由勾股定理得出AB2﹣BD2=AD2,AC2﹣CD2=AD2,得出AB2﹣BD2=AC2﹣CD2,整理得出a2+b2=c2+2aCD,即可得出结论;
(3)作AD⊥BC于D,则BD=BC+CD=a+CD,由勾股定理得出AD2=AB2=BD2,AD2=AC2﹣CD2,得出AB2﹣BD2=AC2﹣CD2,整理即可得出结论;
二、分两种情况:①当∠C为钝角时,由以上(3)得:![]() <c<a+b,即可得出结果;②当∠B为钝角时,得:b﹣a<c<
<c<a+b,即可得出结果;②当∠B为钝角时,得:b﹣a<c<![]() ,即可得出结果.
,即可得出结果.
试题解析:一、解:(1)∵∠C为直角,BC=a,CA=b,AB=c,
∴a2+b2=c2;
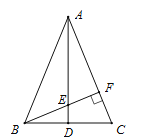
(2)作AD⊥BC于D,如图1所示:
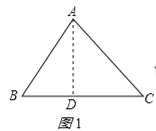
则BD=BC﹣CD=a﹣CD,
在△ABD中,AB2﹣BD2=AD2,
在△ACD中,AC2﹣CD2=AD2,
∴AB2﹣BD2=AC2﹣CD2,
∴c2﹣(a﹣CD)2=b2﹣CD2,
整理得:a2+b2=c2+2aCD,
∵a>0,CD>0,
∴a2+b2>c2;
(3)作AD⊥BC于D,如图2所示:
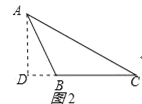
则BD=BC+CD=a+CD,
在△ABD中,AD2=AB2=BD2,
在△ACD中,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,
∴c2﹣(a+CD)2=b2﹣CD2,
整理得:a2+b2=c2﹣2aCD,
∵a>0,CD>0,
∴a2+b2<c2;
二、解:当∠C为钝角时,由以上(3)得:![]() <c<a+b,
<c<a+b,
即5<c<7;
当∠B为钝角时,得:b﹣a<c<![]() ,
,
即1<c<![]() ;
;
综上所述:第三边c的取值范围为5<c<7或1<c<![]() .
.

 阅读快车系列答案
阅读快车系列答案