题目内容
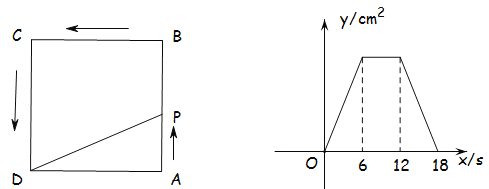
【题目】如图①,在正方形![]() 中,点
中,点![]() 以
以![]() 的速度从点
的速度从点![]() 出发按箭头方向运动,到达点
出发按箭头方向运动,到达点![]() 停止.
停止. ![]() 的面积
的面积![]() 与运动时间
与运动时间![]() 之间的函数图像如图②所示.(规定:点
之间的函数图像如图②所示.(规定:点![]() 在点
在点![]() ,
, ![]() 时,
时, ![]() )
)
发现:(1) ![]() = _______
= _______ ![]() ,当
,当![]() 时,
时, ![]() =_________
=_________ ![]() ;
;
(2)当点![]() 在线段_________上运动时,
在线段_________上运动时, ![]() 的值保持不变.
的值保持不变.
拓展:求当![]() 及
及![]() 时,
时, ![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
探究:当![]() 为多少时,
为多少时, ![]() 的值为
的值为![]() ?
?
【答案】(1)y=3x(0<x<6);y=-3x+54(12<x<18);(2)①x=5;②x=13.
【解析】分析:(1)从图2中看到刚好6s时y最大,得到点P在AB上运动的时间,从而得到AB,x=17时,点P在CD边上,且PD=1即可;
(2)由图2面积没变的是中间一段,从而得到点P在BC上时,y值不变;
拓展:先判断点P在那段线段上运动,用三角形的面积公式计算即可;
探究:y是15时,得到点P在AB和CD这两段线段上,所以直接代入函数关系式中即可.
本题解析:(1)由图2,得到点P在AB上运动时间为6,
∵点P以1cm/s的速度运动,
∴AB=6÷1=6,
∵正方形ABCD,
∴AB=BC=CD=6,
当x=17(s)时,点P在线段CD上,PD=1,
∴y=![]() AD×PD=
AD×PD=![]() ×6×1=3,
×6×1=3,
故答案为6,3,
(2)∵△PAD的边AD时定值6,
∴点P到AD的距离不变时,△PAD的面积不变,
∴点P在BC上,
故答案为BC;
拓展:当0<x<6时,点P在线段AB上,PD=x,
∴y=![]() AD×PD=
AD×PD=![]() ×6×x=3x,
×6×x=3x,
当12<x<18时,点P在线段CD上,PD=18x,
∴y=![]() AD×PD=
AD×PD=![]() ×6×(18x)=543x,
×6×(18x)=543x,
探究:∵y的值等于15cm![]()
把y=15代入y=3x中,得15=3x,
∴x=5,
把y=15代入y=543x中,得15=543x,
∴x=13,
∴当x=5或13s时,y的值等于15.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案