题目内容
【题目】如图,半圆O的直径AC=2 ![]() ,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为 .
,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为 . 
【答案】2 ![]() ﹣2或
﹣2或 ![]() ﹣1
﹣1
【解析】解:①如图1, 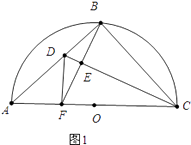
当∠DFE=∠BCE时,
∵∠DEF=∠BEC,
∴△DEF∽△BEC,
∵AC是直径,
∴∠ABC=90°,
∵BF⊥CD,
∴∠CEB=90°,
∴∠BCE+∠CBE=90°,∠DBE+∠EBC=90°,
∴∠DBE=∠BCE=∠DFE,
∴DB=DF,
∵DE⊥BF,
∴EB=EF,
∴BC=CF,
∵点B为半圆的中点,
∴AB=BC,
∴∠A=45°,
∵∠DBF=∠DFB,∠CBF=∠CFB,∠DBF+∠CBF=90°,
∴∠DFB+∠CFB=90°,
∴∠DFC=∠DFA=90°,
∴∠A=∠ADF=45°,
∴AF=DF=BD,
在RT ![]() 中,∵AC=2
中,∵AC=2 ![]() ,
,
∴AB=BC= ![]() AC=2,
AC=2,
∴FC=2,
∴BD=AF=AC﹣FC=2 ![]() ﹣2,
﹣2,
②如图2, 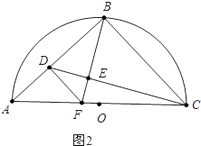
当∠FDE=∠BCE时,
∵∠DEF=∠BEC,
∴△DEF∽△CEB,DF∥BC,
∴∠ADF=∠ABC=90°,
∵∠ABC=∠BEC=90°,
∴∠BCE+∠CBE=90°,∠DBE+∠EBC=90°,
∴∠DBE=∠BCE=∠FDE,
∵∠BDF=∠DBC=90°,∠DBF=∠BCD,
∴△BDF∽△CBD,
∴ ![]() ,
,
∵∠A=45°,∠ADF=90°,
∴∠AFD=∠A=45°,
∴AD=DF,
设BD=x,由(1)可知:AB=BC=2,AD=DF=2﹣x,
∴ ![]() ,整理得:x2+2x﹣4=0,
,整理得:x2+2x﹣4=0,
解得:x=﹣1+ ![]() (或﹣1﹣
(或﹣1﹣ ![]() 舍弃)
舍弃)
∴BD= ![]() ﹣1.
﹣1.
所以答案是2 ![]() ﹣2或
﹣2或 ![]() ﹣1.
﹣1.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对相似三角形的判定的理解,了解相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

 优学名师名题系列答案
优学名师名题系列答案【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?