题目内容
【题目】如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F: ![]() 与直线x=-2交于点P.
与直线x=-2交于点P.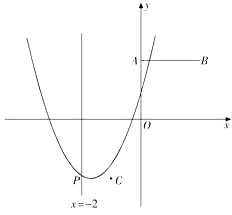
(1)当抛物线F经过点C时,求它的表达式;
(2)抛物线F上有两点M ![]() 、N
、N ![]() ,若-2≤
,若-2≤ ![]() ,
, ![]() <
< ![]() ,求m的取值范围;
,求m的取值范围;
(3)设点P的纵坐标为 ![]() ,求
,求 ![]() 的最小值,此时抛物线F上有两点M
的最小值,此时抛物线F上有两点M ![]() 、N
、N ![]() ,
,
若 ![]() ≤-2,比较
≤-2,比较 ![]() 与
与 ![]() 的大小;
的大小;
(4)当抛物线F与线段AB有公共点时,直接写出m的取值范围。
【答案】
(1)
解:∵抛物线F经过点C(-1,-2),
∴ ![]() .
.
∴m=-1.
∴抛物线F的表达式是 ![]()
(2)
解:抛物线F的对称轴为:直线x=m,
当x≥m时,y随x的增大而增大;
点M、N均在直线x=-2的右侧,
∴直线x=-2必须在直线x=m右侧或与之重合
∴m≤-2
(3)
解:方法一:当x=-2时, ![]() =
= ![]() .
.
∴当m=-2时, ![]() 的最小值=-2.
的最小值=-2.
此时抛物线F的表达式是 ![]() .
.
∴当 ![]() 时,y随x的增大而减小.
时,y随x的增大而减小.
∵ ![]() ≤-2,
≤-2,
∴ ![]() >
> ![]() .
.
方法二:当直线x=-2与抛物线F的对称轴(直线x=m)重合时,
![]() 有最小值,此时m=-2
有最小值,此时m=-2
此时抛物线F的表达式是 ![]() .
.
∴当 ![]() 时,y随x的增大而减小.
时,y随x的增大而减小.
∵ ![]() ≤-2,
≤-2,
∴ ![]() >
> ![]() .
.
(4)![]()
或 ![]() .
.
【解析】(4)解:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),
∴![]() 或
或![]() ,
,
解得:-2≤m≤0或2 ≤ m ≤ 4 .
所以答案是:-2≤m≤0或2 ≤ m ≤ 4 .
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目