题目内容
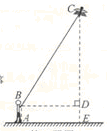
(本题12分)在梯形ABCD中,AB∥CD,∠BCD=90,且AB=1,BC=2,tan∠ADC=2;对角线相交于O点,等腰直角三角板的直角顶点落在梯形的顶点C上,使三角板绕点C旋转。

(1)当三角板旋转到图1的位置时,猜想DE与BF的数量关系,并加以证明。
(2)在(1)问条件下,若BE:CE=1:2,∠BEC=135°,求sin∠BFE的值。
(3)当三角板的一边CF与梯形对角线AC重合时,作DH⊥PE于H,如图2,若OF=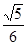 时,求PE及DH的长。
时,求PE及DH的长。

(1)当三角板旋转到图1的位置时,猜想DE与BF的数量关系,并加以证明。
(2)在(1)问条件下,若BE:CE=1:2,∠BEC=135°,求sin∠BFE的值。
(3)当三角板的一边CF与梯形对角线AC重合时,作DH⊥PE于H,如图2,若OF=
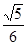 时,求PE及DH的长。
时,求PE及DH的长。(1)当三角板旋转到图1的位置时, DE=BF,证明略。
(2)sin∠BFE=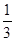 。
。
(3)PE= , DH=
, DH= 。
。
(2)sin∠BFE=
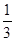 。
。(3)PE=
 , DH=
, DH= 。
。分析:
(1)相等,证DE与BF所在的三角形全等即可;
(2)易得∠BEF=90°,那么可得到△BEF各边的比值进而求解;
(3)根据△CFP∽△CDO,利用相似三角形的性质解答。
解答:
(1)当三角板旋转到图1的位置时,DE=BF,
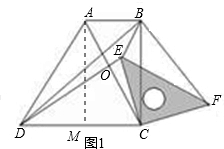
∵∠ECB+∠BCF=90°,∠DCE+∠ECB=90°,
∴∠DCE=∠BCF.
∵∠BCD=90°,AB∥CD
∴∠ABC=90°,∠BAC=∠ACD,
∵BC=2,AB=1,
∴tan∠BAC=2,
∵tan∠ADC=2,
∴∠BAC=∠ADC,
∴∠ACD=∠ADC,
∴AD=AC,
作AM⊥CD于点M,
∴CD=2MC=2AB=2,
∴CD=BC.
∵EC=CF,
∴△DCE≌△BCF.
∴DE=BF。
(2)∵∠BEC=135°,∠FEC=45°,
∴∠BEF=90°.
∵BE:CE=1:2,
∴BE:EF=1:2
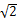 .
.∴sin∠BFE=BE:BF=1/3。
(3)

∵△CFP∽△CDO,
CF:CD=CP:CO=PF:DO
AC=
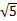 ,
,AO:CO=1:2,CO=2
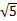 /3,
/3,CF=2
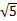 /3-
/3-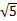 /6=
/6=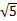 /2,
/2,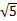 /2:2=CP:2
/2:2=CP:2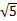 /3,
/3,CP=5/6,
∵DB=2
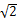 ,BO:DO=1:2,
,BO:DO=1:2,∴DO=4
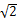 /3,
/3,∴PF=
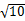 /3,PE=
/3,PE=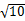 /6。
/6。DP=2-5/6=7/6,
作CN垂直PF于N,
DH:CN=DP:CP,
得DH:7
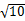 /20。
/20。点评:两条线段相等,通常是证这两条线段所在的三角形全等;注意使用已得到的结论。

练习册系列答案
相关题目

 长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为
长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为 . 据此数据计算,求:中国馆到世博轴其中一端的距离是多少?.
. 据此数据计算,求:中国馆到世博轴其中一端的距离是多少?.
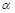 为锐角, sin(
为锐角, sin( )="0.625," 则cos
)="0.625," 则cos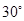 的斜坡上两树间的水平距离AC为
的斜坡上两树间的水平距离AC为 ,则两树间的坡面距离AB为
,则两树间的坡面距离AB为




 ,那么A、B两点的距离为( )
,那么A、B两点的距离为( ) 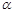 , B .a·tan
, B .a·tan C. a·cos
C. a·cos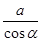

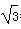 ≈1.73).
≈1.73).