题目内容
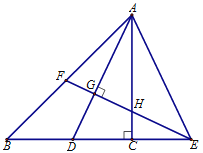
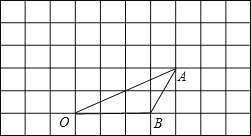
【题目】如图，点O、B、A坐标分别为(0，0)、(3，0)、(4，2)，将△OAB向上平移1个单位长度得到△O′A′B′．
（1）画出△O′A′B′，并写出点A′、B′的坐标；
（2）求△OAB与△O′A′B′重叠部分的面积．
【答案】（1）见解析，A'(4，3)，B'(3，1)；（2）
【解析】
（1）分别找出O、A、B相应的对应点O′、A′、B′的坐标，然后依次连接即可得到三角形；
（2）重叠部分是三角形，且与△OAB相似，根据相似三角形的面积的比等于相似比的平方列式求解即可．
解：（1）△O′A′B′如图所示，
A'（4，3），B'（3，1）；
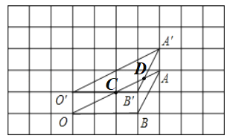
（2）由题意可得：△CDB'∽△OAB，
∴
∵S△OAB＝
×3×2＝3，
∴S△CDB′＝
×3＝．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
【题目】某商场计划销售某种产品，现邀请生产该产品的甲、乙两个厂家进场试销10天．两个厂家提供的返利方案如下：甲厂家每天固定返利70元，且每卖出一件产品厂家再返利2元；乙厂家无固定返利，卖出40件以内（含40件）的产品，每件产品厂家返利4元，超出40件的部分每件返利6元．两个厂家销售情况如下表：
甲厂家销量（件） | 38 | 39 | 40 | 41 | 42 |
天数 | 2 | 4 | 2 | 1 | 1 |
乙厂家销量（件） | 38 | 39 | 40 | 41 | 42 |
天数 | 1 | 2 | 2 | 4 | 1 |
（1）现从乙厂家试销的10天中随机抽取1天，求这1天的返利不超过160元的概率；
（2）商场拟甲、乙两个厂家中选择一个长期销售，如果仅从日返利额的角度考虑，请利用所学的统计学知识为商场作出选择，并说明理由．
