题目内容
【题目】我们定义:对角线互相垂直的四边形叫做垂美四边形.

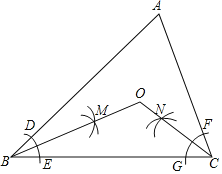
(1)如图1,垂美四边形ABCD的对角线AC,BD交于O.求证:AB2+CD2=AD2+BC2;
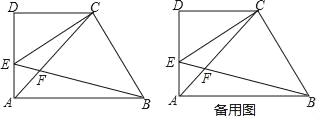
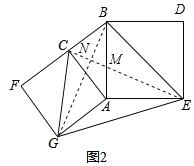
(2)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结BE,CG,GE.
①求证:四边形BCGE是垂美四边形;
②若AC=4,AB=5,求GE的长.
【答案】(1)见解析;(2)①见解析;②GE=![]()
【解析】
(1)由垂美四边形得出AC⊥BD,则∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得AD2+BC2=AO2+DO2+BO2+CO2,AB2+CD2=AO2+BO2+CO2+DO2,即可得出结论;
(2)①连接BG、CE相交于点N,CE交AB于点M,由正方形的性质得出AG=AC,AB=AE,∠CAG=∠BAE=90°,易求∠GAB=∠CAE,由SAS证得△GAB≌△CAE,得出∠ABG=∠AEC,由∠AEC+∠AME=90°,得出∠ABG+∠AME=90°,推出∠ABG+∠BMN=90°,即CE⊥BG,即可得出结论;
②垂美四边形得出CG2+BE2=CB2+GE2,由勾股定理得出BC=![]() =3,由正方形的性质得出CG=4
=3,由正方形的性质得出CG=4![]() ,BE=5
,BE=5![]() ,则GE2=CG2+BE2-CB2=73,即可得出结果.
,则GE2=CG2+BE2-CB2=73,即可得出结果.
(1)证明:∵垂美四边形ABCD的对角线AC,BD交于O,
∴AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得:AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AD2+BC2=AB2+CD2;
(2)①证明:连接BG、CE相交于点N,CE交AB于点M,如图2所示:
∵正方形ACFG和正方形ABDE,
∴AG=AC,AB=AE,∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB和△CAE中,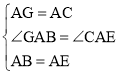 ,
,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,
∵∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,
∴∠ABG+∠BMN=90°,即CE⊥BG,
∴四边形BCGE是垂美四边形;
②解:∵四边形BCGE是垂美四边形,
∴由(1)得:CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=![]() =
=![]() =3,
=3,
∵正方形ACFG和正方形ABDE,
∴CG=![]() AC=4
AC=4![]() ,BE=
,BE=![]() AB=5
AB=5![]() ,
,
∴GE2=CG2+BE2﹣CB2=(4![]() )2+(5
)2+(5![]() )2﹣32=73,
)2﹣32=73,
∴GE=![]() .
.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.