题目内容
【题目】“绿水青山就是金山银山”，随着生活水平的提高，人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理
、
两种型号的净水器，每台型净水器比每台型净水器进价多200元，用5万元购进型净水器与用4.5万元购进型净水器的数量相等.
（1）求每台型、型净水器的进价各是多少元；
（2）槐荫公司计划购进、两种型号的净水器共50台进行试销，其中型净水器为
台，购买资金不超过9.8万元.试销时型净水器每台售价2500元，型净水器每台售价2180元.槐荫公司决定从销售型净水器的利润中按每台捐献
元作为公司帮扶贫困村饮水改造资金，设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
，求的最大值.
【答案】（1）
型净水器每台进价2000元，
型净水器每台进价1800元.（2）
的最大值是
元.
【解析】（1）设A型净水器每台的进价为m元，则B型净水器每台的进价为（m-200）元，根据数量=总价÷单价结合用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等，即可得出关于m的分式方程，解之经检验后即可得出结论；
（2）根据购买资金=A型净水器的进价×购进数量+B型净水器的进价×购进数量结合购买资金不超过9.8万元，即可得出关于x的一元一次不等式，解之即可得出x的取值范围，由总利润=每台A型净水器的利润×购进数量+每台B型净水器的利润×购进数量-a×购进A型净水器的数量，即可得出W关于x的函数关系式，再利用一次函数的性质即可解决最值问题．
（1）设A型净水器每台的进价为m元，则B型净水器每台的进价为（m-200）元，
根据题意得：
，
解得：m=2000，
经检验，m=2000是分式方程的解，
∴m-200=1800．
答：A型净水器每台的进价为2000元，B型净水器每台的进价为1800元．
（2）根据题意得：2000x+1800（50-x）≤98000，
解得：x≤40．
W=（2500-2000）x+（2180-1800）（50-x）-ax=（120-a）x+19000，
∵当70＜a＜80时，120-a＞0，
∴W随x增大而增大，
∴当x=40时，W取最大值，最大值为（120-a）×40+19000=23800-40a，
∴W的最大值是（23800-40a）元．
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
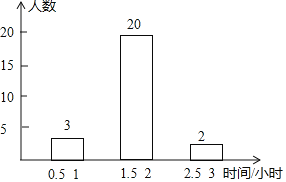
芒果教辅暑假天地重庆出版社系列答案
【题目】某校七年级开展了为期一周的“敬老爱亲”社会活动，并根据学生做家务的时间来评价他们在活动中的表现，学校随机抽查了部分学生在这次活动中做家务的时间，并绘制了如下的频数分布表和频数分布直方图．请根据图表中提供的信息，解答下列问题：
等级 | 做家务时间（小时） | 频数 | 百分比 |
A | 0.5≤x＜1 | 3 | 6% |
B | 1＜x＜1.5 | a | 30% |
C | 1.5≤x＜2 | 20 | 40% |
D | 2≤x＜2.5 | b | m |
E | 2.5≤x＜3 | 2 | 4% |
（1）这次活动中抽查的学生有______人，表中a=______，b=______，m=______，并补全频数分布直方图；
（2）若该校七年级有700名学生，请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有多少人？
【题目】从2开始的连续偶数相加，它们和的情况如下表：
加数的个数（n） | 和（S） |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=12=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
… | … |
（1）根据表中的规律，直接写出2+4+6+8+10+12+14=________
（2）根据表中的规律猜想：S=2+4+6+8+…+2n=___________（用n的代数式表示）；
（3）利用上题中的公式计算102+104+106+…+200的值（要求写出计算过程）．
