题目内容
【题目】已知
是
的函数，自变量的取值范围为
，下表是与的几组对应值
| 0 | 1 | 2 | 3 | 3.5 | 4 | 4.5 | … |
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | … |
小明根据学习函数的经验，利用上述表格所反映出的与之间的变化规律，对该函数的图象与性质进行了探究.下面是小明的探究过程，请补充完整：
(1)如图，在平面直角坐标系中，指出了以上表中各对对应值为坐标的点. 根据描出的点，画出该函数的图象.
(2)根据画出的函数图象填空.
①该函数图象与轴的交点坐标为_____.
②直接写出该函数的一条性质.
【答案】(1)见解析；(2)①(5，0)；②见解析.
【解析】
（1）根据坐标，连接点即可得出函数图像；
（2）①根据图像，当x≥3时，根据两点坐标可得出函数解析式，进而可得出与
轴的交点坐标；
②根据函数图像，相应的自变量的取值范围，可得出其性质.
(1) 如图：
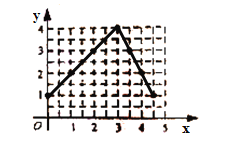
(2)①(5，0)
根据图像，当x≥3时，函数图像为一次函数，
设函数解析式为
，将（3,4）和（4，2）两点代入，即得
解得
即函数解析式为
与x轴的交点坐标为（5,0）；
②答案不唯一．如下几种答案供参考：
当0≤x≤3时，函数值y随x值增大而增大；
当x≥3时，函数值y随x值增大而减小；
当x=3时，函数有最大值为4；
该函数没有最小值．
练习册系列答案
相关题目
【题目】某商家计划从厂家采购空调和冰箱两种产品共
台，空调和冰箱的采购单价与销售单价如表所示：
采购单价 | 销售单价 | |
空调 |
|
|
冰箱 |
|
|
若采购空调
台，且所采购的空调和冰箱全部售完，求商家的利润；
厂家有规定，采购空调的数量不少于
台，且空调采购单价不低于
元，问商家采购空调多少台时总利润最大？并求最大利润．
